题目内容
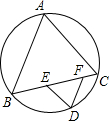 如图.在△ABC的外接圆上,弧AB、弧BC、弧CA的度数比为12:13:11.在BC上取一点D.过点D分别作AC、AB的平行线,交BC于E、F两点,则∠EDF的度数为________.
如图.在△ABC的外接圆上,弧AB、弧BC、弧CA的度数比为12:13:11.在BC上取一点D.过点D分别作AC、AB的平行线,交BC于E、F两点,则∠EDF的度数为________.
65°
分析:首先设△ABC的外接圆的圆心为O,连接OA,OB,OC,由弧AB、弧BC、弧CA的度数比为12:13:11,即可求得圆心角∠AOB与∠AOC的度数,又由圆周角定理,求得∠ABC与∠ACB的度数,DE∥AC,DF∥AB与三角形的内角和定理,即可求得∠EDF的度数.
解答: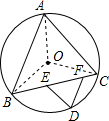 解:设△ABC的外接圆的圆心为O,连接OA,OB,OC,
解:设△ABC的外接圆的圆心为O,连接OA,OB,OC,
∵弧AB、弧BC、弧CA的度数比为12:13:11,
∴∠AOB= ×360°=120°,∠AOC=
×360°=120°,∠AOC= =110°,
=110°,
∴∠ACB= ∠AOB=60°,∠ABC=
∠AOB=60°,∠ABC= ∠AOC=55°,
∠AOC=55°,
∵DE∥AC,DF∥AB,
∴∠FED=∠ACB=60°,∠DFE=∠ABC=55°,
∴∠EDF=180°-∠DEF-∠DFE=180°-60°-55°=65°.
故答案为:65°.
点评:此题考查了圆周角定理、平行线的性质以及三角形内角和定理.此题难度适中,解题的关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.注意辅助线的作法.
分析:首先设△ABC的外接圆的圆心为O,连接OA,OB,OC,由弧AB、弧BC、弧CA的度数比为12:13:11,即可求得圆心角∠AOB与∠AOC的度数,又由圆周角定理,求得∠ABC与∠ACB的度数,DE∥AC,DF∥AB与三角形的内角和定理,即可求得∠EDF的度数.
解答:
 解:设△ABC的外接圆的圆心为O,连接OA,OB,OC,
解:设△ABC的外接圆的圆心为O,连接OA,OB,OC,∵弧AB、弧BC、弧CA的度数比为12:13:11,
∴∠AOB=
 ×360°=120°,∠AOC=
×360°=120°,∠AOC= =110°,
=110°,∴∠ACB=
 ∠AOB=60°,∠ABC=
∠AOB=60°,∠ABC= ∠AOC=55°,
∠AOC=55°,∵DE∥AC,DF∥AB,
∴∠FED=∠ACB=60°,∠DFE=∠ABC=55°,
∴∠EDF=180°-∠DEF-∠DFE=180°-60°-55°=65°.
故答案为:65°.
点评:此题考查了圆周角定理、平行线的性质以及三角形内角和定理.此题难度适中,解题的关键是掌握圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.注意辅助线的作法.

练习册系列答案
 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
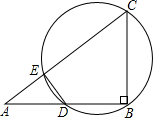 (在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)
(在下面的(I)(II)两题中选做一题,若两题都做,按第(I)题评分)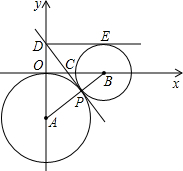 上,过P点作两圆的公切线DP交y轴于D,交x轴于C,
上,过P点作两圆的公切线DP交y轴于D,交x轴于C,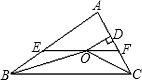 如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+
如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过点O作EF∥BC交AB于E,交AC于F,过点O作OD⊥AC于D.下列四个结论:①∠BOC=90°+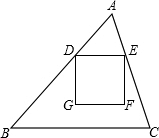 如图,在△ABC中,BC=12,AB=10,sinB=
如图,在△ABC中,BC=12,AB=10,sinB= 如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°.
如图,在△ABC中,AB=AC,∠BAC=30°,分别以AB、AC为边向形外作两个等腰直角三角形ABD和ACE,使∠BAD=∠CAE=90°. 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.