题目内容
16.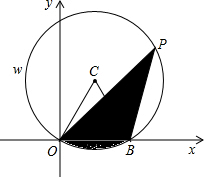 如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)
如图,在平面直角坐标系xOy中,⊙C经过点O,交x轴的正半轴于点B(2,0),P是$\widehat{OwB}$上的一个动点,且∠OPB=30°.设P点坐标为(m,n)(1)当n=2$\sqrt{3}$,求m的值;
(2)设图中阴影部分的面积为S,求S与n之间的函数关系式,并求S的最大值;
(3)试探索动点P在运动过程中,是否存在整点P(m,n)(横、纵坐标都为整数的点叫整点)?若存在,请求出;若不存在,请说明理由.
分析 (1)根据圆周角定理得到∠BCO=2∠BPO=60°,则可判断△OCB为等边三角形,则OC=OB=2,作CF⊥OB于F,交$\widehat{OwB}$于E,如图,根据垂径定理得到OF=BF=1,则可根据勾股定理计算出CF=$\sqrt{3}$,于是得到C(1,$\sqrt{3}$),然后利用两点间的距离公式得到(1-m)2+($\sqrt{3}$-2$\sqrt{3}$)2=22,再解方程即可得到即m的值;
(2)利用S=S弓形OB+S△POB=S扇形BOC-S△BOC+S△PBC和扇形面积公式得到S═n+$\frac{2}{3}$π-$\sqrt{3}$,根据一次函数性质得n最大时,S最大,而当点P为$\widehat{OwB}$的中点时,n最大,易得n的最大值为2+$\sqrt{3}$,然后把n=2+$\sqrt{3}$代入解析式即可S的最大值;
(3)过C点作直径MN∥x轴,易得M(-1,$\sqrt{3}$),N(3,$\sqrt{3}$),则-1≤m≤3,由于当m=-1和3时,n=$\sqrt{3}$;n=0和2时,n=2$\sqrt{3}$;当n=1时,n=2+$\sqrt{3}$,即P点的横坐标为整数,纵坐标都不是整数,由此可判断动点P在运动过程中,不存在整点P(m,n).
解答 解:(1)∵∠BCO=2∠BPO=2×30°=60°,
而CB=CO,
∴△OCB为等边三角形,
∴OC=OB=2
作CF⊥OB于F,交$\widehat{OwB}$于E,如图,则OF=BF=1,
∴CF=$\sqrt{O{C}^{2}-O{F}^{2}}$=$\sqrt{3}$,
∴C(1,$\sqrt{3}$),
∵CP=2,
∴(1-m)2+($\sqrt{3}$-2$\sqrt{3}$)2=22,解得m=0或m=2,
即m的值为0或2;
(2)S=S弓形OB+S△POB
=S扇形BOC-S△BOC+S△PBC
=$\frac{60•π•{2}^{2}}{360}$-$\frac{1}{2}$•2•$\sqrt{3}$+$\frac{1}{2}$×2•n
=n+$\frac{2}{3}$π-$\sqrt{3}$
当点P为$\widehat{OwB}$的中点时,n最大,S最大,
即当n=2+$\sqrt{3}$,S的最大值=2+$\sqrt{3}$+$\frac{2}{3}$π-$\sqrt{3}$=2+$\frac{2}{3}$π;
(3)动点P在运动过程中,不存在整点P(m,n).利用如下:
过C点作直径MN∥x轴,
∵MC=NC=2,
而C(1,$\sqrt{3}$),
∴M(-1,$\sqrt{3}$),N(3,$\sqrt{3}$),
∴-1≤m≤3,
∵当m=-1和3时,n=$\sqrt{3}$;n=0和2时,n=2$\sqrt{3}$;当n=1时,n=2+$\sqrt{3}$,
∴当P点的横坐标为整数时,纵坐标都不是整数,
∴动点P在运动过程中,不存在整点P(m,n).
点评 本题考查了圆的综合题:熟练掌握垂径定理、圆周角定理和等边三角形的性质;会利用勾股定理和两点间的距离公式计算线段的长;理解坐标与图形性质;会利用规则图形的面积的和差计算不规则图形的面积.

| A. | -3 | B. | |-4| | C. | -$\frac{1}{3}$ | D. | $\frac{1}{3}$ |
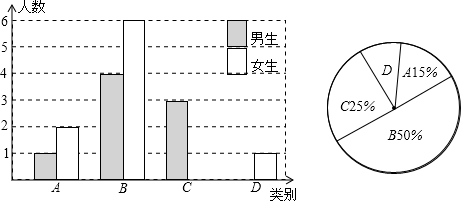
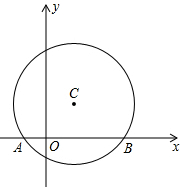 如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧$\widehat{AB}$上.
如图,在平面直角坐标系中,以点C(1,1)为圆心,2为半径作圆,交x轴于A,B两点,点P在优弧$\widehat{AB}$上.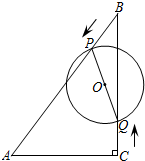 如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.
如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0≤t≤2),连接PQ,以PQ为直径作⊙O.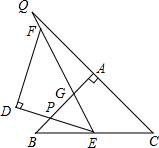 如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.
如图,△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.若AQ=12,BP=3,则PG=5.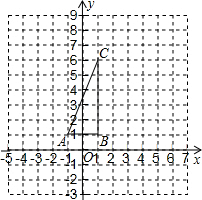 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,1),B(1,1),C(1,6).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-1,1),B(1,1),C(1,6).