Question

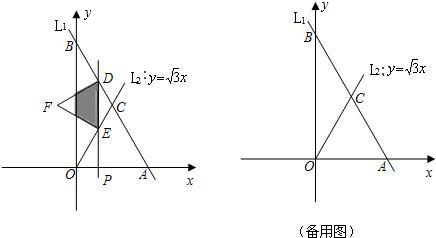
如图，直线l₁分别交x轴、y轴于A、B两点，且AO=8，BO=8

3

，与直线y=

3

x交于点C．平行于y轴的直线L₂从原点O出发，以每秒1个单位长度的速度沿x轴向右平移，到C点时停止；l₂分别交线段BC、OC、x轴于点D、E、P，以DE为边向左侧作等边△DEF，设直线l₂的运动时间为t（秒）．
（1）直接写出直线l₁的解析式；
（2）以D、E、O、F为顶点的多边形能否为梯形，若能，求出此时t的值；若不能，请说明理由；
（3）设△DEF与△BCO重叠部分的面积为S（平方单位），试探究：S与t的函数关系式．

Answer 1

分析：（1）当x=0，y=OB，当y=0，求得k值，从而求得直线表达式；
（2）依题意P点横坐标为x即为t，根据l₁，l₂的解析式表示DE的长，当F点落在y轴上时，四边形DEOF为梯形，此时P点横坐标为DE的二分之根号3倍，列方程求解；
（3）以P点落在y轴为分界，求出分界时，t的值，按照P点在△BOC外，P点在△BOC内，两种情况，求得面积的表达式．

解答：解：（1）设直线1为y=kx+b，
当x=0时，y=b=OB=8

3

，
当y=0时，-8

3

=8k，则k=-

3

，
所以直线为：y=-

3

x+8

3

①；

（2）当F在y轴上时，OFDE四点成为梯形，
设P（x，0），
∵直线y=

3

x，
∴∠EOP=60°，
∴OE=2OP，
∴OE=2x，
则DE=

2 3 x

3

，
由（1）所得DE=-

3

x+8

3

-

3

x=-2

3

x+8

3

，
解得x=3即t=3；

（3）设点P的横坐标为x_P，
∵直线1y=-

3

x+8

3

与直线y=

3

x交于点C，
∴C（4，4

3

）；
当x_P=0时，则S=0；
当0＜x_P＜3时，
由以上DE=-2

3

t+8

3

，
梯形的上底=DE-2DM=-2

3

t+8

3

-

2 3 t

3

，
所以面积S=

1

2

×(DE+HN)t=-

7 3 t2

3

+ 8

3

t．
当3≤x_P＜4时，△DEF与△BCO重叠部分的面积为△DEF的面积，
∴S=

1

2

×DE×FV
=（-

3

t+4

3

）×（-3t+12）
=3

3

t²-24

3

t+48

3

．

点评：本题考查了一次函数的综合运用，（1）当x=0，y=OB，当y=0，求得k值，从而求得直线表达式．（2）依题意P点横坐标为x即为t，根据l₁，l₂的解析式表示DE的长，当F点落在y轴上时，四边形DEOF为梯形，从而列式计算得．（3）当P在y轴或者在三角形BOC外，则S=0；P点在△BOC内，两种情况，部分求面积的表达式．