Question

19．如图，△ABC中，∠ACB=90°，sinB=$\frac{\sqrt{3}}{2}$，BC=1，点D为斜边AB的中点，过A、C、D三点作⊙O，点P为AC所对的优弧上任意一点，点M、N分别为线段AC、AP的中点，则MN的最大值为1．

Answer 1

分析 先判断出三角形AOD是等边三角形，再求出OA=1，从而只要CP最大，MN最大，圆中最大的弦是直径，进而求出CP即可．

解答 解：如图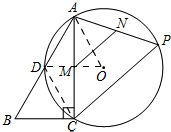

连接OA，OD，CD，
在Rt△ABC中，BC=1，sinB=$\frac{\sqrt{3}}{2}$，
∴AB=2，∠B=60°，
∴∠BAC=30°，
∵点D是直角三角形ABC斜边AB中点，
∴AD=CD=1，
∵点M是AC中点，
∴OD必过点M，
∴OD⊥AC，
∴∠ADO=60°，
∵OD=OA，
∴△AOD是等边三角形，
∴OA=1，
∵点M、N分别为线段AC、AP的中点，
∴MN=$\frac{1}{2}$CP，
要MN最大，则CP最大，
而CP是圆的弦，
∴CP是圆的直径时最大，
即CP最大=2OA=2，
∴MN最大=1．
故答案为1．

点评 此题是三角形的外接圆与外心，主要考查了圆的性质，直角三角形的性质，等边三角形的判定和性质，锐角三角函数，解本题的关键是求出圆的半径OA=1．