题目内容
7.先化简($\frac{x+2}{{x}^{2}-2x}$+$\frac{8}{4-{x}^{2}}$)÷$\frac{x-2}{x}$,再求当x=$\sqrt{2}-1$时,此代数式的值.分析 原式括号中两项通分并利用同分母分式的加法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=[$\frac{x+2}{x(x-2)}$-$\frac{8}{(x+2)(x-2)}$]•$\frac{x}{x-2}$=$\frac{(x+2)^{2}-8x}{x(x+2)(x-2)}$•$\frac{x}{x-2}$=$\frac{(x-2)^{2}}{x(x+2)(x-2)}$•$\frac{x}{x-2}$=$\frac{1}{x+2}$,
当x=$\sqrt{2}$-1时,原式=$\frac{1}{\sqrt{2}+1}$=$\sqrt{2}$-1.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.若关于x的方程$\frac{x+2}{x-1}=\frac{m+1}{x-1}$产生增根,则m是( )
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
19.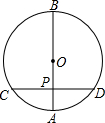 如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )
 如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )
如图,在⊙O中,直径AB垂直于弦CD,垂足为P.若PA=2,PB=8,则CD的长为( )| A. | 2$\sqrt{5}$ | B. | 4 | C. | 8 | D. | $4\sqrt{5}$ |
16.下列说法中,不正确是( )
| A. | 对角线互相平分的四边形是平行四边形 | |
| B. | 两组对角分别相等的四边形是平行四边形 | |
| C. | 一组对边平行且相等的四边形是平行四边形 | |
| D. | 一组对边平行另一组对边相等的四边形是平行四边形 |
17.一件工作甲单独做a小时完成,乙单独做b小时完成,甲、乙两人一起完成这项工作需要的小时数是( )
| A. | $\frac{ab}{a+b}$ | B. | $\frac{1}{a+b}$ | C. | $\frac{1}{a}$+$\frac{1}{b}$ | D. | $\frac{1}{ab}$ |
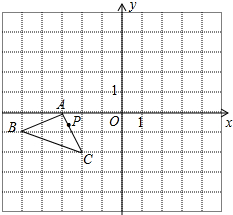 如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+5,b+4)
如图,在平面直角坐标系中,P(a,b)是△ABC的边AC上一点,△ABC经平移后点P的对应点为P1(a+5,b+4)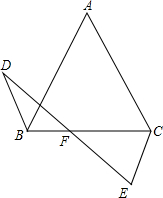 如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.
如图所示,△ABC中,AB=AC,点D在△ABC的外部,且∠ABD是锐角,点E在射线AC的左侧,且∠ACE与∠ABD互补,BD=CE,DE与BC相交于点F.