题目内容
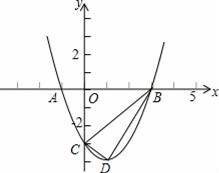
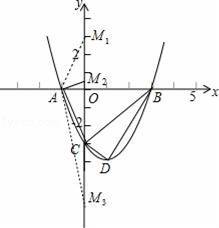
如图,已知抛物线y=ax2+bx﹣3与x轴的一个交点为A(﹣1,0),另一个交点为B,与y轴的交点为C,其顶点为D,对称轴为直线x=1.
(1)求抛物线的解析式;
(2)已知点M为y轴上的一个动点,当△ACM是以AC为一腰的等腰三角形时,求点M的坐标.

【考点】抛物线与x轴的交点;二次函数图象上点的坐标特征;待定系数法求二次函数解析式.
【专题】计算题.
【分析】(1)利用对称性可得B(3,0),则利用交点式得抛物线解析式为y=a(x+1)(x﹣3)=ax2﹣2ax﹣3a,所以﹣3a=3,解得a=1,于是得到抛物线解析式为y=x2﹣2x﹣3;
(2)分类讨论:当AC=AM时,易得点M1(0,3),如图;②当CM=CA时,先计算出AC=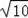
 ,再以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,易得M2(0,
,再以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,易得M2(0,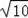
 ﹣1),M3(0,﹣
﹣1),M3(0,﹣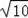
 ﹣3).
﹣3).
【解答】解:(1)∵点A(﹣1,0)和点B关于直线x=1对称,
∴B(3,0),
∴抛物线解析式为y=a(x+1)(x﹣3)=ax2﹣2ax﹣3a,
∴﹣3a=3,解得a=1,
∴抛物线解析式为y=x2﹣2x﹣3;
(2)当AC=AM时,点M1与点C关于x轴对称,则M1(0,3),如图;
②当CM=CA时,AC=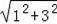
 =
=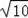
 ,
,
以C点为圆心,CA为半径画弧交y轴于M2,M3,如图,则OM2=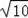
 ﹣1,OM3=OC+CM3=3+
﹣1,OM3=OC+CM3=3+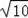
 ,则M2(0,
,则M2(0,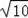
 ﹣1),M3(0,﹣
﹣1),M3(0,﹣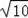
 ﹣3).
﹣3).
综上所述,满足条件的点M的坐标为(0,3),(0,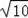
 ﹣1),(0,﹣
﹣1),(0,﹣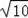
 ﹣3).
﹣3).

【点评】本题考查了抛物线与x轴的交点:把求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标问题转化为解关于x的一元二次方程.解决(2)小题的关键是利用等腰三角形的性质画出点M的坐标.

练习册系列答案
相关题目