Question

如图，已知数轴上点A表示的为8，B是数轴上一点，且AB=14，动点P从点A出发，以每秒5个单位长度的速度沿数轴向左匀速运动，设运动时间为t（t＞0）秒．

（1）写出数轴上点B表示的数　　　　　　，点P表示的数　　　　　　（用含t的代数式表示）；

（2）动点H从点B出发，以每秒3个单位长度的速度沿数轴向左匀速运动，若点P、H同时出发，问点P运动多少秒时追上点H？

Answer 1

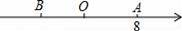
【考点】一元一次方程的应用；数轴．

【专题】几何动点问题．

【分析】（1）先计算出线段OB，则可得到出点B表示的数；利用速度公式得到PA=5t，易得P点表示的数为8﹣5t；

（2）点P比点H要多运动14个单位，利用路程相差14列方程得5t=14+3t，然后解方程即可．

【解答】解：（1）∵OA=8，AB=14，

∴OB=6，

∴点B表示的数为﹣6，

∵PA=5t，

∴P点表示的数为8﹣5t，

故答案为﹣6，8﹣5t；

（2）根据题意得5t=14+3t，

解得t=7．

答：点P运动7秒时追上点H．

【点评】本题考查了一元二次方程的应用：利用方程解决实际问题的基本思路如下：首先审题找出题中的未知量和所有的已知量，直接设要求的未知量或间接设一关键的未知量为x，然后用含x的式子表示相关的量，找出之间的相等关系列方程、求解、作答，即设、列、解、答．