题目内容
 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则DB的长为
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则DB的长为
- A.

- B.

- C.
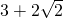
- D.

A
分析:先根据图形旋转的性质求出BE的长,再根据勾股定理求出DB的长即可.
解答:∵Rt△BDE由Rt△ABC旋转而成,∠ACB=∠E=90°,AC=3,DE=5,
∴AC=BE=3,
在Rt△BDE中,
∵BE=3,DE=5,
∴DB= =
= =
= .
.
故选A.
点评:本题考查的是图形旋转的性质,熟知图形旋转不变性的性质是解答此题的关键.
分析:先根据图形旋转的性质求出BE的长,再根据勾股定理求出DB的长即可.
解答:∵Rt△BDE由Rt△ABC旋转而成,∠ACB=∠E=90°,AC=3,DE=5,
∴AC=BE=3,
在Rt△BDE中,
∵BE=3,DE=5,
∴DB=
 =
= =
= .
.故选A.
点评:本题考查的是图形旋转的性质,熟知图形旋转不变性的性质是解答此题的关键.

练习册系列答案
相关题目
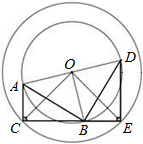 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为( )
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为( )A、5+
| ||||
B、4
| ||||
C、3+2
| ||||
D、4+
|
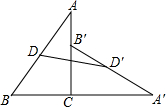 如图将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,已知AC=12cm,BC=5cm,则线段DD′的长为
如图将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置,D,D′分别是AB,A′B′的中点,已知AC=12cm,BC=5cm,则线段DD′的长为 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则OC的长为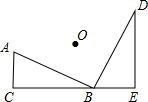 如图,Rt△ABC绕O点逆时针旋转90°得Rt△BDE,其中∠ABD=∠ACB=∠BED=90°,AC=3,DE=5,则OC的长为( )
如图,Rt△ABC绕O点逆时针旋转90°得Rt△BDE,其中∠ABD=∠ACB=∠BED=90°,AC=3,DE=5,则OC的长为( )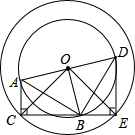 如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则DB的长为( )
如图,Rt△ABC绕O点旋转90°得Rt△BDE,其中∠ACB=∠E=90°,AC=3,DE=5,则DB的长为( )