Question

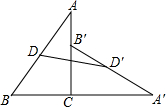如图将Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，D，D′分别是AB，A′B′的中点，已知AC=12cm，BC=5cm，则线段DD′的长为

 

cm．

Answer 1

分析：先利用勾股定理求出AB的长，根据直角三角形斜边上的中线等于斜边的一半的性质求出CD=

1

2

AB，然后连接CD、CD′，再根据旋转的性质求出∠DCD′=90°，CD=CD′，再利用勾股定理列式求解即可．

解答：解：∵AC=12cm，BC=5cm，
∴AB=

AC2+BC2

=

122+52

=13，
∵D是AB的中点，
∴CD=

1

2

AB=

1

2

×13=

13

2

，
∵Rt△ABC绕直角顶点C顺时针方向旋转90°到△A′B′C的位置，
∴∠B′CD′=∠BCD，
∵∠BCD+∠DCB′=90°，
∴∠B′CD′+DCB′=90°，
又CD=CD′（旋转后是对应边），
∴△CDD′是等腰直角三角形，
∴DD′=

2

CD=

13 2

2

cm．
故答案为：

13 2

2

．

点评：本题考查了旋转的性质，直角三角形斜边上的中线等于斜边的一半的性质，勾股定理的应用，根据题意判断出旋转后△CDD′是等腰直角三角形是解题的关键．