题目内容
9. 一副直角三角板如图放置,点A在ED上,∠F=∠ACB=90°,∠E=30°,∠B=45°,AC=12,试求BD的长.
一副直角三角板如图放置,点A在ED上,∠F=∠ACB=90°,∠E=30°,∠B=45°,AC=12,试求BD的长.
分析 先解Rt△ABC,由∠ACB=90°,∠B=45°,得出BC=AC=12.再解Rt△ACD,求出∠ADC=90°-∠E=60°,根据三角函数定义得到CD=$\frac{AC}{tan60°}$=4$\sqrt{3}$,那么BD=BC-DC=12-4$\sqrt{3}$.
解答 解:∵在Rt△ABC中,∠ACB=90°,∠B=45°,
∴BC=AC=12.
∵在Rt△ACD中,∠ACD=90°,∠ADC=90°-∠E=60°,
∴CD=$\frac{AC}{tan60°}$=4$\sqrt{3}$,
∴BD=BC-DC=12-4$\sqrt{3}$.
点评 本题考查了解直角三角形,锐角三角函数的定义,求出BC与DC的长是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.下列计算正确的是( )
| A. | -22=4 | B. | 32=6 | C. | (-1)3=-1 | D. | -|-1|=1 |
4.某商品经过两次降价,零售价降为原来的$\frac{1}{2}$,已知两次降价的百分率均为x,则列出方程正确的是( )
| A. | ${(1+x)^2}=\frac{1}{2}$ | B. | ${(1-x)^2}=\frac{1}{2}$ | C. | (1+x)2=2 | D. | (1-x)2=2 |
 如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行.
如图,若∠A=∠DCE 则AB∥CD,理由是同位角相等,两直线平行. 如图,在△ABC中,AB=BC,∠ABC=90°,F为BC上一点,M为AF的中点,BE平分∠ABC,且EF⊥BE,求证:CF=2ME.
如图,在△ABC中,AB=BC,∠ABC=90°,F为BC上一点,M为AF的中点,BE平分∠ABC,且EF⊥BE,求证:CF=2ME.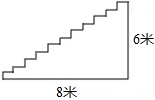 如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?
如图,凯瑞酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是2米,楼梯的总长度为8米,总高度为6米,已知这种地毯每平方米的售价是60元.请你帮老板算下,购买地毯多少钱?