题目内容
12.若m>n,则下面的不等关系错误的是( )| A. | m-5>n-5 | B. | 2m+4>2n+4 | C. | 6m>6n | D. | -$\frac{1}{3}$m$>-\frac{1}{3}$n |
分析 根据不等式的基本性质逐个进行判断即可.
解答 解:A、∵m>n,
∴m-5>n-5,故本选项错误;
B、∵m>n,
∴2m>2n,
∴2m+4>2n+4,故本选项错误;
C、∵m>n,
∴6m>6n,故本选项错误;
D、∵m>n,
∴-$\frac{1}{3}$m<-$\frac{1}{3}$n,故本选项正确;
故选D.
点评 本题考查了对不等式的基本性质的应用,能理解不等式的基本性质的内容是解此题的关键.

练习册系列答案
相关题目
3.下列等式成立的是( )
| A. | $\sqrt{7}$-$\sqrt{2}$=$\sqrt{5}$ | B. | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ | C. | $\sqrt{{2}^{2}+{3}^{2}}$=5 | D. | -$\sqrt{(-5)^{2}}$=5 |
20.计算(2ab2)3,结果正确的是( )
| A. | 2a3b6 | B. | 6a3b6 | C. | 8a3b5 | D. | 8a3b6 |
7.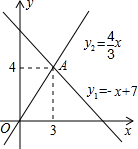 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
 如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )
如图,一次函数y1=-x+7与正比例函数y2=$\frac{4}{3}$x的图象交于点A,若y1>y2,则自变量x的取值范围是( )| A. | x>3 | B. | x<3 | C. | x>4 | D. | x<4 |
 如图,在一块长AB=a cm,宽BC=b cm的长方形草地上,有三条宽都是2m的小路,则这块草地的绿地面积为(a-4)(b-2)cm2.
如图,在一块长AB=a cm,宽BC=b cm的长方形草地上,有三条宽都是2m的小路,则这块草地的绿地面积为(a-4)(b-2)cm2.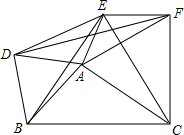 如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,且∠BAC≠60°.
如图,以△ABC的三边为边在BC的同一侧分别作三个等边三角形,即△ABD、△BCE、△ACF,且∠BAC≠60°.