题目内容
5.在弹性限度内,弹簧伸长的长度与所挂物体的重量成正比,某弹簧能挂的重物不超过10kg,且挂重6kg时,弹簧长度为13cm,挂重2kg时,弹簧的长度为11cm,求弹簧挂重后的长度y(单位:cm)与所挂重物x(单位:kg)之间的函数关系式,并画出这个函数的图象.分析 首先设出一次函数解析式,进而利用待定系数法求一次函数解析式即可.
解答  解:∵挂重6kg时,弹簧长度为13cm,挂重2kg时,弹簧的长度为11cm,
解:∵挂重6kg时,弹簧长度为13cm,挂重2kg时,弹簧的长度为11cm,
设y与x的函数表达式为:y=kx+b,
∴$\left\{\begin{array}{l}{13=6k+b}\\{11=2k+b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=10}\end{array}\right.$,
∴y与x的函数表达式为:y=$\frac{1}{2}$x+10.
函数的图象如图所示,
点评 此题主要考查了一次函数的应用,待定系数法求一次函数解析式,得出k,b的值是解题关键.

练习册系列答案
相关题目
15.下列式子中,不能用平方差公式计算的是( )
| A. | (a+b)(a-b) | B. | (x2-y2)(x2+y2) | C. | (1-x)(1+x) | D. | (a-b)(b-a) |
 如图,△ABC中,AB=AC,AD=BC,AD平分∠BAC,交BC于点D.延长BC使得BC=2CE,过点E作EF⊥CE且EF=CE.连接AF,点H在线段AF上,且满足∠ACD=∠HCE.
如图,△ABC中,AB=AC,AD=BC,AD平分∠BAC,交BC于点D.延长BC使得BC=2CE,过点E作EF⊥CE且EF=CE.连接AF,点H在线段AF上,且满足∠ACD=∠HCE.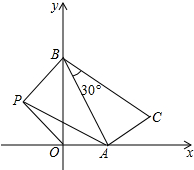 如图,一次函数y=-$\sqrt{3}x+\sqrt{3}$的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,使∠ABC=30°;
如图,一次函数y=-$\sqrt{3}x+\sqrt{3}$的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,使∠ABC=30°;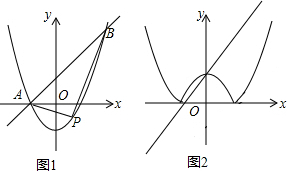
 如图,对称轴为x=1的抛物线经过A(-1,0),B(4,5)两点.
如图,对称轴为x=1的抛物线经过A(-1,0),B(4,5)两点.