题目内容
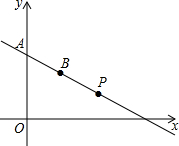 如图,在平面直角坐标系中,已知A(0,4),B(2,3).
如图,在平面直角坐标系中,已知A(0,4),B(2,3).(1)求出直线AB的解析式;
(2)点P是直线AB上的一个动点,在平面直角坐标系内,是否存在另一个点Q,使得以A,O,P,Q为顶点的四边形是菱形(AP为其中一个边)?若存在,请求出点Q的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据待定系数法,可得函数解析式;
(2)分类讨论:菱形APQO,菱形APOQ,根据菱形的四边相等,可得答案.
(2)分类讨论:菱形APQO,菱形APOQ,根据菱形的四边相等,可得答案.
解答:解:(1)设函数解析式为y=kx+b,函数图象经过点A、B,得
,
解得
.
故直线AB的解析式是y=-
x+4;
(2)设P点坐标是(x,-
x+4),
①菱形APQO,得AP=PQ=QO=AQ=4,
即x2+(-
x+4-4)2=16,
解得x1=
或x=-
,
y1=-
+4,y2=
+4
P1(
,-
+4),P2(-
,
+4).
P1Q1=4,P1Q1∥y轴,得
Q1(
,-
).
P2Q2=4,P2Q2∥y轴,得
Q2(-
,
).
②菱形APOQ,AP=OP=PQ=AQ,
PQ在AO的垂直平分线上,得
P3、Q3的纵坐标是2.
当y=2时,-
x+4=2,解得x=4,P3(4,2).
P3、Q3关于y轴对称,Q3(-4,2);
综上所述:Q1(
,-
),Q2(-
,
),Q3(-4,2).
|
解得
|
故直线AB的解析式是y=-
| 1 |
| 2 |
(2)设P点坐标是(x,-
| 1 |
| 2 |
①菱形APQO,得AP=PQ=QO=AQ=4,
即x2+(-
| 1 |
| 2 |
解得x1=
8
| ||
| 5 |
8
| ||
| 5 |
y1=-
4
| ||
| 5 |
4
| ||
| 5 |
P1(
8
| ||
| 5 |
4
| ||
| 5 |
8
| ||
| 5 |
4
| ||
| 5 |
P1Q1=4,P1Q1∥y轴,得
Q1(
8
| ||
| 5 |
4
| ||
| 5 |
P2Q2=4,P2Q2∥y轴,得
Q2(-
8
| ||
| 5 |
4
| ||
| 5 |
②菱形APOQ,AP=OP=PQ=AQ,
PQ在AO的垂直平分线上,得
P3、Q3的纵坐标是2.
当y=2时,-
| 1 |
| 2 |
P3、Q3关于y轴对称,Q3(-4,2);
综上所述:Q1(
8
| ||
| 5 |
4
| ||
| 5 |
8
| ||
| 5 |
4
| ||
| 5 |
点评:本题考查了一次函数综合题,利用了待定系数法求解析式,利用了菱形的性质:菱形对边平行,菱形的四边相等.

练习册系列答案
相关题目
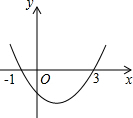 已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b+2a=0②abc<0③a-2b+4c<0④8a+c>0,其中正确的有( )
已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(-1,0),(3,0),对于下列命题:①b+2a=0②abc<0③a-2b+4c<0④8a+c>0,其中正确的有( )| A、3个 | B、2个 | C、1个 | D、0个 |
以下列各组线段为边作三角形,不能构成直角三角形的是( )
A、1,
| ||||||
B、
| ||||||
| C、5,12,13 | ||||||
| D、9,40,41 |
若x2+kx+16能通过因式分解写成(a+b)2的形式,则k的值是( )
| A、8 | B、-8 | C、±8 | D、±4 |
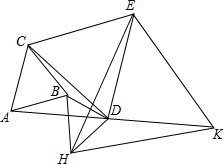 如图,位于同一平面内的正△ABC、正△CDE和正△EHK(顶点依逆时针方向排列),两两地有公共点C和E,且D是AK的中点,求证:△BHD也是正三角形.
如图,位于同一平面内的正△ABC、正△CDE和正△EHK(顶点依逆时针方向排列),两两地有公共点C和E,且D是AK的中点,求证:△BHD也是正三角形.