题目内容
9.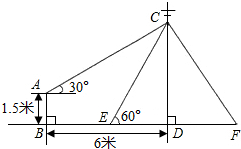 如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在电线杆上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置测角仪AB,在A处测得电线杆上C处的仰角为30°,已知测角仪高AB为1.5米,求拉线CE的长(结果精确到0.1米,参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
分析 过点A作AH⊥CD,垂足为H,在Rt△ACH中求出CH,在Rt△ECD中,再求出EC即可.
解答 解:过点A作AH⊥CD,垂足为H,
由题意可知四边形ABDH为矩形,∠CAH=30°,
∴AB=DH=1.5,BD=AH=6,
在Rt△ACH中,tan∠CAH=$\frac{CH}{AH}$,
∴CH=AH•tan∠CAH,
∴CH=AH•tan∠CAH=6tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$,
∵DH=1.5,
∴CD=2$\sqrt{3}$+1.5,
在Rt△CDE中,
∵∠CED=60°,sin∠CED=$\frac{CD}{CE}$,
∴CE=$\frac{CD}{sin60°}$=4+$\sqrt{3}$≈5.7(米),
答:拉线CE的长约为5.7米.
点评 本题考查直角三角形的应用-仰角俯角问题,矩形的判定和性质、锐角三角函数等知识,解题的关键是学会添加常用辅助线.构造直角三角形解决问题,属于中考常考题型.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
4.如图,在平面直角坐标系xOy中,点A(1,0),B(2,0),正六边形ABCDEF沿x轴正方向无滑动滚动,每旋转60°为滚动1次,那么当正六边形ABCDEF滚动2017次时,点F的坐标是( )


| A. | (2017,0) | B. | (2017$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | C. | (2018,$\sqrt{3}$) | D. | (2018,0) |
14. 如图,是某几何体的俯视图,则该几何体可能是( )
如图,是某几何体的俯视图,则该几何体可能是( )
 如图,是某几何体的俯视图,则该几何体可能是( )
如图,是某几何体的俯视图,则该几何体可能是( )| A. |  | B. |  | C. |  | D. |  |
18.下列各数中,比-3大1的数是( )
| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
19.3-π的绝对值是( )
| A. | 3-π | B. | π-3 | C. | 3 | D. | π |
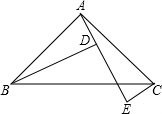 如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.
如图,A、D、E三点在同一直线上,且△BAD≌△ACE,∠ABD=30°,∠ADB=80°.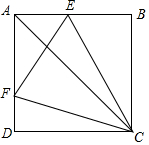 如图,E,F分别是边长为a的正方形ABCD的边AB,AD上的点,∠ECF=45°.
如图,E,F分别是边长为a的正方形ABCD的边AB,AD上的点,∠ECF=45°.
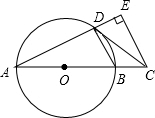 如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.
如图,AB是⊙O的直径,点C在AB的延长线上,CD与⊙O相切于点D,CE⊥AD,交AD的延长线于点E.