题目内容
(14分)如图所示,过点F(0,1)的直线y=kx+b与抛物线 交于M(x1,
交于M(x1,y1)和N(x2,y2)两点(其中x1<0,x2<0).
⑴求b的值.
⑵求x1•x2的值
⑶分别过M、N作直线l:y=-1的垂线,垂足分别是M1、N1,判断△M1FN1的形状,并证明你的结论.
⑷对于过点F的任意直线MN,是否存在一条定直线m,使m与以MN为直径的圆相切.如果有,请法度出这条直线m的解析式;如果没有,请说明理由.


解:⑴b=1
⑵显然
 和
和 是方程组
是方程组 的两组解,解方程组消元得
的两组解,解方程组消元得 ,依据“根与系数关系”得
,依据“根与系数关系”得 =-4
=-4⑶△M1FN1是直角三角形是直角三角形,理由如下:
由题知M1的横坐标为x1,N1的横坐标为x2,设M1N1交y轴于F1,则F1M1•F1N1=-x1•x2=4,而FF1=2,所以F1M1•F1N1=F1F2,另有∠M1F1F=∠FF1N1=90°,易证Rt△M1FF1∽Rt△N1FF1,得∠M1FF1=∠FN1F1,故∠M1FN1=∠M1FF1+∠F1FN1=∠FN1F1+∠F1FN1=90°,所以△M1FN1是直角三角形.
⑷存在,该直线为y=-1.理由如下:
直线y=-1即为直线M1N1.
如图,设N点横坐标为m,则N点纵坐标为
 ,计算知NN1=
,计算知NN1= , NF=
, NF=
 ,得NN1=NF
,得NN1=NF同理MM1=MF.
那么MN=MM1+NN1,作梯形MM1N1N的中位线PQ,由中位线性质知PQ=
 (MM1+NN1)=
(MM1+NN1)= MN,即圆心到直线y=-1的距离等于圆的半径,所以y=-1总与该圆相切.解析:
MN,即圆心到直线y=-1的距离等于圆的半径,所以y=-1总与该圆相切.解析:略

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 4、如图所示,过点P画直线a的平行线b的作法的依据是( )
4、如图所示,过点P画直线a的平行线b的作法的依据是( ) 两点.
两点.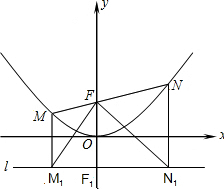 如图所示,过点F(0,1)的直线y=kx+b与抛物线y=
如图所示,过点F(0,1)的直线y=kx+b与抛物线y= 如图所示,过点D分别作DE∥BC,交AC于E,作DF∥AB,交BC于F,若AD:DC=1:2,则△ADE,△DCF,平行四边形DEBF的面积比是( )
如图所示,过点D分别作DE∥BC,交AC于E,作DF∥AB,交BC于F,若AD:DC=1:2,则△ADE,△DCF,平行四边形DEBF的面积比是( ) 如图所示,过点A(1,0)作垂直x轴的直线l,分别交函数y1=x(x≥0),y2=
如图所示,过点A(1,0)作垂直x轴的直线l,分别交函数y1=x(x≥0),y2=