题目内容
1.已知a=$\frac{2-\sqrt{3}}{2+\sqrt{3}}$,b=$\frac{2+\sqrt{3}}{2-\sqrt{3}}$,求a2-ab+b2的值.分析 先化简a,b,再把a,b的值代入求值即可.
解答 解:∵a=$\frac{2-\sqrt{3}}{2+\sqrt{3}}$=$\frac{(2-\sqrt{3})(2-\sqrt{3})}{(2+\sqrt{3})(2-\sqrt{3})}$=7-4$\sqrt{3}$,
b=$\frac{2+\sqrt{3}}{2-\sqrt{3}}$=$\frac{(2+\sqrt{3})^{2}}{(2+\sqrt{3})(2-\sqrt{3})}$=7+4$\sqrt{3}$,
∴a2-ab+b2=(a-b)2+ab=(7-4$\sqrt{3}$-7-4$\sqrt{3}$)2+(7-4$\sqrt{3}$)(7+4$\sqrt{3}$)
=192+49-48
=193.
点评 本题考查了二次根式的化简,掌握分母有理化和完全平方公式是解题的关键.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
13.在△ABC和△A′B′C′中,下面能得到△ABC≌△A′B′C′的条件是( )
| A. | AB=A′B′,AC=A′C,∠B=∠B′ | B. | AB=A′B′,BC=B′C,∠A=∠A′ | ||
| C. | AC=A′C′,BC=B′C′,∠C=∠C′ | D. | AC=A′C′,BC=B′C′,∠B=∠B′ |
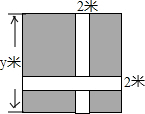 如图,小区在边长为y米的正方形内,修宽为2米的通道,其余部分种草.
如图,小区在边长为y米的正方形内,修宽为2米的通道,其余部分种草.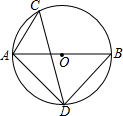 如图,AB是⊙O的直径,∠ACD=45°,∠ADC=30°.
如图,AB是⊙O的直径,∠ACD=45°,∠ADC=30°.
 如图,已知AB为⊙O的弦,从圆上任一点引弦CD⊥AB,作∠OCD的平分线交⊙O于点P,连接PA、PB,求证:PA=PB.
如图,已知AB为⊙O的弦,从圆上任一点引弦CD⊥AB,作∠OCD的平分线交⊙O于点P,连接PA、PB,求证:PA=PB.