Question

已知BD是△ABC的中线，AC=6，且∠ADB=45°，∠C=30°，则AB=（　　）

• A、

  6

• B、2

  3

• C、3

  2

• D、6

Answer 1

分析：根据题中所给的条件，在直角三角形中解题．根据角的正切值与三角形边的关系，结合勾股定理求解．

解答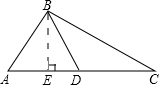：解：过点B作BE⊥AC交AC于点E．
设BE=x，
∵∠BDA=45°，∠C=30°，
∴DE=x，BC=2x，
∵tan∠C=

BE

CE

，
∴

x

3+x

=tan30°，
∴3x=（3+x）

3

，解得x=

3+3 3

2

，
在Rt△ABE中，AE=3-

3+3 3

2

=

3-3 3

2

，
由勾股定理得：AB²=BE²+AE²，AB=

( 3+3 3 2 )2+( 3-3 3 2 )2

=3

2

．
故选C．

点评：本题考查了解直角三角形中三角函数的应用，要熟练掌握好边角之间的关系．