题目内容
已知:如图,在△ABC中,AB=AC,∠A=45°,点D在AC上,DE⊥AB于E,且DE=DC,连结EC.请写出图中所有 等腰三角形(△ABC除外),并说明理由.
等腰三角形(△ABC除外),并说明理由.
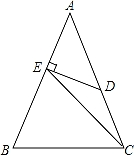
【考点】等腰三角形的判定与性质.
【分析】根据等腰直角三角形的性质得到∠ADE=45°,推出∠A=∠ADE,得到△AED为等腰直角三角形,由DE=DC,得到△DEC为等腰三角形,根据∠BEC=180°﹣90°﹣22.5°67.5°,证得∠B=67.5°,得到∠B=∠BEC,得到△BEC为等腰三角形.
【解答】解:等腰三角形△AED,△DEC,△BEC,
证明:∵∠A=45°,DE⊥AB于E,
∴∠AED=90°,
∴∠ADE=45°,
∴∠A=∠ADE,
∴AE=DE,
∴△AED为等腰直角三角形,
∵DE=DC,
∴△DEC为等腰三角形,
∵∠BEC=180°﹣90°﹣22.5°=67.5°,
又∵∠A=45°,AE=AC,
∴∠B=67.5°,
∴∠B=∠BEC,
∴BC=EC,
∴△BEC为等腰三角形.
【点评】本题考查了等腰直角三角形的判定和性质,三角形的内角和,垂直的定义.熟练掌握等腰三角形的判定是解题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
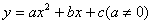 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论: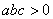 ;②
;② 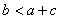 ;③
;③ 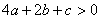 ;
;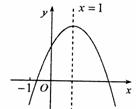 ④
④ 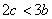 ; ⑤
; ⑤ 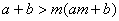 ,(
,(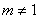 的实数)
的实数)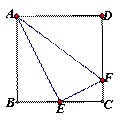
 .
. 的值.
的值.
 .
. D.﹣
D.﹣ ,与x轴相交于M、N两点.如果点M的坐标为
,与x轴相交于M、N两点.如果点M的坐标为 ,求点N的坐标.
,求点N的坐标.
 ,
, ,则x、y的大小关系是
,则x、y的大小关系是