题目内容
如图,在平面直角坐标系xOy中,⊙A与y轴相切于点 ,与x轴相交于M、N两点.如果点M的坐标为
,与x轴相交于M、N两点.如果点M的坐标为 ,求点N的坐标.
,求点N的坐标.

【考点】切线的性质;坐标与图形性质;勾股定理;垂径定理.
【分析】连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,根据切线性质得出AB=AM=R,求出CM=R﹣ ,AC=
,AC=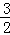 ,MN=2CM,
,MN=2CM,
由勾股定理得出方程R2=(R﹣ )2+(
)2+(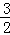 )2,求出方程的解即可.
)2,求出方程的解即可.
【解答】解: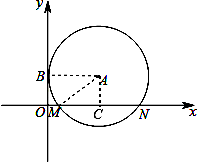
连接AB、AM、过A作AC⊥MN于C,设⊙A的半径是R,
∵⊙A与y轴相切于B,
∴AB⊥y轴,
∵点 ,与x轴相交于M、N两点,点M的坐标为
,与x轴相交于M、N两点,点M的坐标为 ,
,
∴AB=AM=R,CM=R﹣ ,AC=
,AC=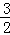 ,MN=2CM,
,MN=2CM,
由勾股定理得:R2=(R﹣ )2+(
)2+(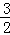 )2,
)2,
R=2.5,
∴CM=CN=2.5﹣ =2,
=2,
∴ON= +2+2=4
+2+2=4 ,
,
即N的坐标是(4 ,0).
,0).
【点评】本题考查了切线的性质,勾股定理,垂径定理的应用,关键是能根据题意得出关于R的方程.

练习册系列答案
相关题目
 ,AC=__________.
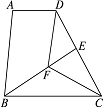
,AC=__________. 等腰三角形(△ABC除外),并说明理由.
等腰三角形(△ABC除外),并说明理由.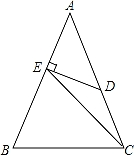
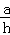 =k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .
=k,我们把k叫做这个菱形的“形变度”.若变形后的菱形有一个角是60°,则形变度k= .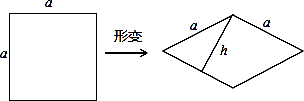
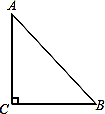








 B.
B. C.
C. D.
D.