题目内容
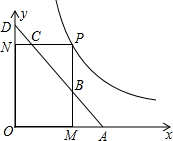 如图,动线段AD所在的直线方程是y=-x+b(b>0),矩形OMPN的一个顶点P在双曲线y=
如图,动线段AD所在的直线方程是y=-x+b(b>0),矩形OMPN的一个顶点P在双曲线y=| 4 |
| x |
考点:反比例函数图象上点的坐标特征,等腰直角三角形,矩形的性质
专题:
分析:首先过C作x轴的垂线,过B点作y轴的垂线,设P(x,y),根据AD的直线解析式可得DO=AO,进而得出AC•BD=2xy求出即可.
解答: 解:如图所示:过C作x轴的垂线垂足为F,过B点作y轴的垂线垂足为E,
解:如图所示:过C作x轴的垂线垂足为F,过B点作y轴的垂线垂足为E,
设P(x,y),
∵动线段AD所在的直线方程是y=-x+b,
∴DO=AO,
∴△AOD是等腰直角三角形,
∴∠DCN=∠MBA=45°,
∴∠PCB=∠PBC=45°,
∴CP=PB,BE=ED=x,CF=AF=y,
∴AC=
y,DB=
x,
∴AC•BD=2xy=8,
故答案为:8.
 解:如图所示:过C作x轴的垂线垂足为F,过B点作y轴的垂线垂足为E,
解:如图所示:过C作x轴的垂线垂足为F,过B点作y轴的垂线垂足为E,设P(x,y),
∵动线段AD所在的直线方程是y=-x+b,
∴DO=AO,
∴△AOD是等腰直角三角形,
∴∠DCN=∠MBA=45°,
∴∠PCB=∠PBC=45°,
∴CP=PB,BE=ED=x,CF=AF=y,
∴AC=
| 2 |
| 2 |
∴AC•BD=2xy=8,
故答案为:8.
点评:此题主要考查了反比例函数图象上点的坐标性质以及等腰直角三角形的性质等知识,得出AC=
y,DB=
x是解题关键.
| 2 |
| 2 |

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
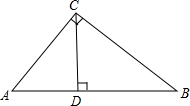 如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,设∠ACD=α,∠BCD=β,AC=8,BC=6,分别求cosα和tanβ的值.
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,设∠ACD=α,∠BCD=β,AC=8,BC=6,分别求cosα和tanβ的值. 如图,在△OAB中,∠ABO=45°,顶点A在反比例函数y=
如图,在△OAB中,∠ABO=45°,顶点A在反比例函数y=