题目内容
18.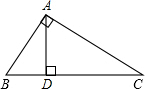 如图,△ABC中,∠BAC=90°,AD是△ABC的高,∠C=30°,BC=4,求BD的长.
如图,△ABC中,∠BAC=90°,AD是△ABC的高,∠C=30°,BC=4,求BD的长.
分析 在直角△ABC中,根据“30度角所对的直角边等于斜边的一半”求得AB=$\frac{1}{2}$BC=2;然后在直角△ABD中,根据“30度角所对的直角边等于斜边的一半”求得BD=$\frac{1}{2}$AB=1.
解答 解:如图,∵在△ABC中,∠BAC=90°,∠C=30°,AD是高,
∴∠ADB=90°,∠BAD=∠C=30°,
∴在直角△ABC中,AB=$\frac{1}{2}$BC=2,
∴在直角△ABC中,BD=$\frac{1}{2}$AB=1.
∴BD的长为1.
点评 本题考查了含30度角的直角三角形.应用时,要注意找准30°的角所对的直角边和斜边是解题的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
6.已知a=-(0.2)2,b=-2-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则a、b、c、d的大小关系是( )
| A. | a<b<d<c | B. | b<a<d<c | C. | a<b<c<d | D. | b<a<c<d |
10.-2的相反数是( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
7.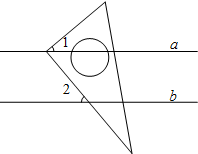 如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,则∠2等于( )
如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,则∠2等于( )
 如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,则∠2等于( )
如图,直线a与直线b平行,将三角板的直角顶点放在直线a上,若∠1=40°,则∠2等于( )| A. | 40° | B. | 50° | C. | 60° | D. | 140° |
8.若m与3互为相反数,则|m-3|的值为( )
| A. | 0 | B. | 6 | C. | $\frac{10}{3}$ | D. | $\frac{8}{3}$ |
 如图,AB∥CD,∠A=∠D,判断AF与ED的位置关系,并说明理由.
如图,AB∥CD,∠A=∠D,判断AF与ED的位置关系,并说明理由.