题目内容
已知菱形两条对角线长的比为3:4,设边长为x,面积为y,求x、y的二次函数关系式.
考点:菱形的性质
专题:
分析:根据菱形的对角线互相垂直平分和勾股定理求得菱形对角线的长度,然后利用菱形的面积公式列出函数解析式.
解答: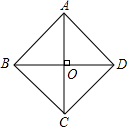 解:如图,在菱形ABCD中,对角线AC与BD相交于O.则AC⊥BD,则AO=
解:如图,在菱形ABCD中,对角线AC与BD相交于O.则AC⊥BD,则AO=
AC,OD=
BD.
∵菱形两条对角线长的比为3:4,设边长为x,
∴AO:OD=3:4,
故设AO=3a,OD=4a.
则由勾股定理知,x2=9a2+16a2=25a2,
解得 a2=
.
则该菱形的面积为:
AO•BD=
×6a×8a=24a2=
x2,即y=
x2.
 解:如图,在菱形ABCD中,对角线AC与BD相交于O.则AC⊥BD,则AO=
解:如图,在菱形ABCD中,对角线AC与BD相交于O.则AC⊥BD,则AO=| 1 |
| 2 |
| 1 |
| 2 |
∵菱形两条对角线长的比为3:4,设边长为x,
∴AO:OD=3:4,
故设AO=3a,OD=4a.
则由勾股定理知,x2=9a2+16a2=25a2,
解得 a2=
| x2 |
| 25 |
则该菱形的面积为:
| 1 |
| 2 |
| 1 |
| 2 |
| 24 |
| 25 |
| 24 |
| 25 |
点评:此题主要考查了菱形的性质,以及勾股定理的应用,关键是掌握菱形四边相等,对角线互相垂直平分.

练习册系列答案
相关题目

 如图,一个圆锥的高是10厘米,侧面展开图是半圆,求圆锥的面积.
如图,一个圆锥的高是10厘米,侧面展开图是半圆,求圆锥的面积.
 如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点,则BE的长为
如图,在矩形ABCD中,AB=8,BC=10,E是AB上一点,将矩形ABCD沿CE折叠后,点B落在AD边的F点,则BE的长为 在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?
在今年第9号超强台风“圣帕”来临之际,B市气象局测得台风中心位于B市正东方向500km的A处,正以20km/h千米的速度向西北方向移动,距台风中心400的范围内受到影响,问B市是否受到这次台风的影响?如果有影响,则持续的时间有多长?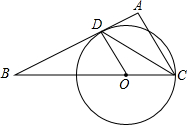 如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C,D两点作⊙O且圆心O在BC上.若CD=5,△ADC的面积为6,求半径.
如图,在△ABC中,∠A=90°,CD平分∠ACB交AB于D,AD<AC,过C,D两点作⊙O且圆心O在BC上.若CD=5,△ADC的面积为6,求半径.