题目内容
等腰△ABC,AB=AC,∠BAC=120°,P为BC的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P,三角板绕P点旋转.

(1)如图a,当三角板的两边分别交AB、AC于点E、F时.求证:△BPE∽△CFP;
(2)操作:将三角板绕点P旋转到图b情形时,三角板的两边分别交BA的延长线、边AC于点E、F.
① 探究1:△BPE与△CFP还相似吗?(只需写出结论)
② 探究2:连结EF,△BPE与△PFE是否相似?请说明理由;
(1)证明过程见解析,(2)①相似 ②相似,理由见解析
解析:(1) 证明:∵在△ABC中,
∠BAC=120°,AB=AC,
∴∠B=∠C=30°.
∵∠B+∠BPE+∠BEP=180°,
∴∠BPE+∠BEP=150°,
∴∠EPF=30°,
又∵∠BPE+∠EPF+∠CPF=180°,
∴∠BPE+∠CPF=150°,
∴∠BEP=∠CPF,
∴△BPE∽△CFP(两角对应相等的两个三角形相似).
(2) ①相似 ②相似
解:①△BPE∽△CFP;②△BPE与△PFE相似.
下面证明结论:
同(1),可证△BPE∽△CFP,得 CP:BE=PF:PE,而CP=BP,因此 BP:BE=PF:PE.
又因为∠EBP=∠EPF,所以△BPE∽△PFE(两边对应成比例且夹角相等的两个三角形相似).

练习册系列答案
相关题目
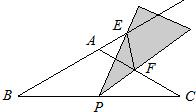 等腰△ABC,AB=AC,∠BAC=120°,P为BC上的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P处,三角板绕点P旋转到如图所示情形时,三角板的两边分别交BA的延长线于点E,交边AC于点F,连接EF,△BPE与△PFE是否相似?请说明理由.
等腰△ABC,AB=AC,∠BAC=120°,P为BC上的中点,小慧拿着含30°角的透明三角板,使30°角的顶点落在点P处,三角板绕点P旋转到如图所示情形时,三角板的两边分别交BA的延长线于点E,交边AC于点F,连接EF,△BPE与△PFE是否相似?请说明理由.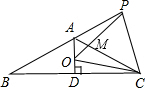 如图,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,OP与AC相交与点M,则下列结论:
如图,在等腰△ABC中AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,OP与AC相交与点M,则下列结论: 已知等腰△ABC,AB=AC=4,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.
已知等腰△ABC,AB=AC=4,∠BAC=120°,请用圆规和直尺作出△ABC的外接圆.并计算此外接圆的半径.