题目内容
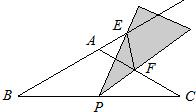等腰△ABC，AB=AC，∠BAC=120°，P为BC上的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P处，三角板绕点P旋转到如图所示情形时，三角板的两边分别交BA的延长线于点E，交边AC于点F，连接EF，△BPE与△PFE是否相似？请说明理由．
分析：先根据已知条件证明△BPE∽△CFP，可得出
=
，然后即可证明△BPE∽△PFE．
| PE |
| PF |
| BE |
| PB |
解答：相似．
证明：∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°．
∵∠B+∠BEP=∠EPC，∠EPF=30°，
∴∠BEP=∠CPF．
∴△BPE∽△CFP．
∴
=
．
∵P为BC上的中点，
∴BP=PC，
∴
=
．
即
=
．
又∵∠B=∠EPF=30°，
∴△BPE∽△PFE．
证明：∵AB=AC，∠BAC=120°，
∴∠B=∠C=30°．
∵∠B+∠BEP=∠EPC，∠EPF=30°，
∴∠BEP=∠CPF．
∴△BPE∽△CFP．
∴
| PC |
| PF |
| BE |
| PE |
∵P为BC上的中点，
∴BP=PC，
∴
| PB |
| PF |
| BE |
| PE |
即
| PE |
| PF |
| BE |
| PB |
又∵∠B=∠EPF=30°，
∴△BPE∽△PFE．
点评：本题考查了相似三角形的判定与性质及等腰三角形的性质，难度适中，关键是掌握相似三角形的判定条件．
练习册系列答案
相关题目
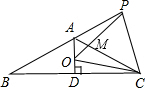如图，在等腰△ABC中AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC，OP与AC相交与点M，则下列结论：
已知等腰△ABC，AB=AC=4，∠BAC=120°，请用圆规和直尺作出△ABC的外接圆．并计算此外接圆的半径．