题目内容
如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．请完成下列填空：
①请在图中确定并点出该圆弧所在圆心D点的位置，圆心D坐标
（2，0）
（2，0）
；②⊙D的半径=
2
| 5 |
2
（结果保留根号）；| 5 |
③若扇形ADC是一个圆锥的侧面展开图，求圆锥的侧面积．
分析：（1）根据圆心到A、B、C距离相等即可得出D点位置，进而得出D点坐标；
（2）根据勾股定理求出AD的长即可；
（3）根据△AOD≌△DEC，得出扇形DAC的圆心角为90°，进而利用扇形面积公式求出即可．
（2）根据勾股定理求出AD的长即可；
（3）根据△AOD≌△DEC，得出扇形DAC的圆心角为90°，进而利用扇形面积公式求出即可．
解答：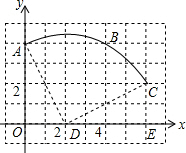
解：（1）如图所示：D即为所求，D（2，0）；
故答案为：（2，0）；
（2）如图，AD=
=
=2
；
故答案为：2
；
（3）作CE⊥x轴，垂足为E，
∵△AOD≌△DEC，
∴∠OAD=∠CDE，
又∵∠OAD+∠ADE=90°，
∴∠CDE+∠ADO=90°，
∴扇形DAC的圆心角为90°，
S扇形=
=
=5π，
即圆锥的侧面积为5π．
解：（1）如图所示：D即为所求，D（2，0）；故答案为：（2，0）；
（2）如图，AD=
| AO2+OD2 |
| 42+22 |
| 5 |
故答案为：2
| 5 |
（3）作CE⊥x轴，垂足为E，
∵△AOD≌△DEC，
∴∠OAD=∠CDE，
又∵∠OAD+∠ADE=90°，
∴∠CDE+∠ADO=90°，
∴扇形DAC的圆心角为90°，
S扇形=
| nπR2 |
| 360 |
90π(2
| ||
| 360 |
即圆锥的侧面积为5π．
点评：此题主要考查了垂径定理和勾股定理以及扇形面积公式应用，根据已知得出D点位置是解题关键．
练习册系列答案
高中必刷题系列答案
相关题目
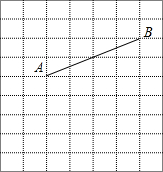如图，在单位长度为1的正方形网格中，把线段AB绕点A顺时针旋转90°得到线段AB′．
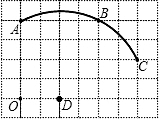如图，在单位长度为1的正方形网格中，一段圆弧经过格点A、B、C．以点O为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系，该圆弧所在圆的圆心为点D．
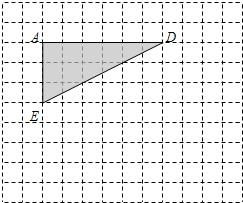如图，在单位长度为1的正方形网格中有一个△DAE（∠DAE=90°）．
作图、证明与计算
（2012•杨浦区二模）如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点A、B、C．