Question

等腰三角形的底角是15°，腰长为10，则其腰上的高为________．

Answer 1

5
分析：根据题意作出图形，利用等腰三角形的两底角相等求出三角形的顶角等于150°，所以顶角的邻补角等于30°，然后根据直角三角形中30°角所对的直角边等于斜边的一半即可求出．
解答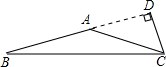：解：如图，△ABC中，∠B=∠ACB=15°，
∴∠BAC=180°-15°×2=150°，
∴∠CAD=180°-150°=30°，
∵CD是腰AB边上的高，
∴CD=AC=×10=5cm．
故答案为：5．
点评：本题考查了等腰三角形的性质与30°所对的直角边等于斜边的一半的性质，根据题意作出图形是解题的关键，对学生来说也是难点．