题目内容
3.阅读下列材料:解答“已知x-y=2,且x>1,y<0,试确定x+y的取值范围”有如下解法:
解:∵x-y=2,又∵x>1,∴y+2>1,即y>-1
又y<0,∴-1<y<0.…①
同理得:1<x<2.…②
由①+②得-1+1<y+x<0+2,∴x+y的取值范围是0<x+y<2.
请按照上述方法,完成下列问题:
已知关于x、y的方程组$\left\{\begin{array}{l}{2x-y=-1}\\{x+2y=5a-8}\end{array}\right.$的解都为非负数.
(1)求a的取值范围;
(2)已知2a-b=1,求a+b的取值范围;
(3)已知a-b=m(m是大于1的常数),且b≤1,求2a+b最大值.(用含m的代数式表示)
分析 (1)先把a当作已知求出x、y的值,再根据x、y的取值范围得到关于a的一元一次不等式组,求出a的取值范围即可;
(2)根据阅读材料所给的解题过程,分别求得a、b的取值范围,然后再来求a+b的取值范围;
(3)根据(1)的解题过程求得a、b取值范围;结合限制性条件得出结论即可.
解答 解:(1)因为关于x、y的方程组$\left\{\begin{array}{l}{2x-y=-1}\\{x+2y=5a-8}\end{array}\right.$的解都为非负数,
解得:$\left\{\begin{array}{l}{x=a-2}\\{y=2a-3}\end{array}\right.$,
可得:$\left\{\begin{array}{l}{a-2≥0}\\{2a-3≥0}\end{array}\right.$,
解得:a≥2;
(2)由2a-b=1,
可得:$\left\{\begin{array}{l}{a=\frac{1+b}{2}}\\{a≥2}\end{array}\right.$,
可得:$\frac{1+b}{2}≥2$,
解得:b≥3,
所以a+b≥5;
(3)$\left\{\begin{array}{l}{a=m+b}\\{a≥2}\end{array}\right.$,
所以m+b≥2,
可得:$\left\{\begin{array}{l}{b≥2-m}\\{b≤1}\end{array}\right.$,
可得:2-m≤b≤1,
同理可得:2≤a≤1+m,
所以可得:6-m≤2a+b≤3+2m,
最大值为3+2m.
点评 本题考查了一元一次不等式组的应用,解答本题的关键是仔细阅读材料,理解解题过程.

练习册系列答案
相关题目
18.下列命题是真命题的是( )
| A. | 有一个角为60°的三角形是等边三角形 | |
| B. | 底边相等的两个等腰三角形全等 | |
| C. | 有一个角是40°,腰相等的两个等腰三角形全等 | |
| D. | 一边上的中线等于这条边的一半的三角形是直角三角形 |
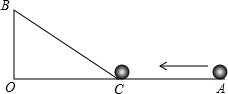 如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?
如图,∠AOB=90°,OA=36cm,OB=12cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?