Question

【题目】在△ABC 中，AB＝AC，点 O 是△ABC 的外心，∠BOC＝60°，BC＝2，则 S△ABC＝_

Answer 1

【答案】

【解析】

仔细分析题目信息，由于不确定点A的位置，故需分点A在△ABC的外接圆的优弧BC上或劣弧BC上，根据题意画出图形；

当点A在△ABC的外接圆的优弧BC上时，记此时的三角形为△A1BC时，连接OB、OC；

根据等边三角形的判定易得△OBC为等边三角形，利用等边三角形的性质及勾股定理不难求得△OBC的高OD的值，那么△A1BC的高也就知晓了；

此时利用三角形的面积公式即可求出△A1BC的面积了；

当点A在△ABC的外接圆的劣弧BC上时，记此时的三角形为△A2BC时，连接OB、OC，此时按照上述方法求出△A2BC的面积即可解答！

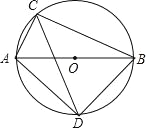
解：根据题意画出图形，

存在两种情况，

①当△ABC为△A1BC时，连接OB、OC，

∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，

∴△OBC为等边三角形，

∴OB=OC=BC=2，OA1⊥BC于点D，

∴CD=1，

∴OD=，

∴A1D=OA1-OD=2-，

∴S△A1BC=BCA1D2=；

②当△ABC为△A2BC时，连接OB、OC，

∵点O是等腰△ABC的外心，且∠BOC=60°，底边BC=2，OB=OC，

∴△OBC为等边三角形，

∴OB=OC=BC=2，OA1⊥BC于点D，

∴CD=1，

∴OD=，

∴A2D=OD+OA2=2+，

∴S△A2BC=BC·A2D2=.

∴△ABC的面积为.