题目内容
学习全等三角形的判定方法以后,我们知道“已知两边和一角分别相等的两个三角形不一定全等”,但下列两种情形还是成立的.
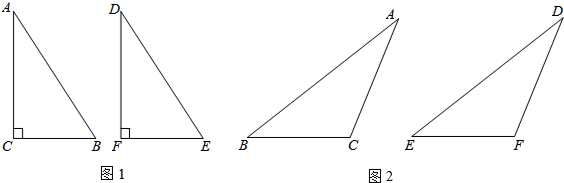
(1)第一情形(如图1)
在△ABC和△DEF中,∠C=∠F=90°,AC=DF,AB=DE,则根据 ,得出△ABC≌△DEF;
(2)第二情形(如图2)在△ABC和△DEF中,∠C=∠F(∠C和∠F均为钝角),AC=DF,AB=DE,求证:△ABC≌△DEF.
(1)第一情形(如图1)
在△ABC和△DEF中,∠C=∠F=90°,AC=DF,AB=DE,则根据
(2)第二情形(如图2)在△ABC和△DEF中,∠C=∠F(∠C和∠F均为钝角),AC=DF,AB=DE,求证:△ABC≌△DEF.

考点:全等三角形的判定,直角三角形全等的判定
专题:
分析:(1)根据直角三角形全等的判定方法HL,可证明△ABC≌△DEF,可得出答案;
(2)可过A作AG⊥BC,交BC的延长线于点G,D点作DH⊥EF,交EF的延长线于点H,可先证明△ACG≌△DFH,可得到AG=DH,再证明△ABG≌△DEH,可得∠B=∠E,可证得结论.
(2)可过A作AG⊥BC,交BC的延长线于点G,D点作DH⊥EF,交EF的延长线于点H,可先证明△ACG≌△DFH,可得到AG=DH,再证明△ABG≌△DEH,可得∠B=∠E,可证得结论.
解答:(1)解:AC、DF为直角边,AB、DE为斜边,且∠C=∠F=90°,
故可根据“HL”可证明△ABC≌△DEF,
故答案为:HL;
(2)证明:如图,过A作AG⊥BC,交BC的延长线于点G,D点作DH⊥EF,交EF的延长线于点H,
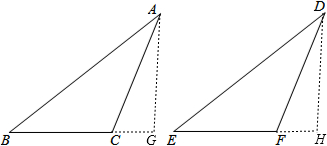
∵∠BCA=∠EFD,
∴∠ACG=∠DFH,
在△ACG和△DFH中,
,
∴△ACG≌△DFH(AAS),
∴AG=DH,
在Rt△ABG和Rt△DEH中,
,
∴△ABG≌△DEH(HL),
∴∠B=∠E,
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
故可根据“HL”可证明△ABC≌△DEF,
故答案为:HL;
(2)证明:如图,过A作AG⊥BC,交BC的延长线于点G,D点作DH⊥EF,交EF的延长线于点H,

∵∠BCA=∠EFD,
∴∠ACG=∠DFH,
在△ACG和△DFH中,
|
∴△ACG≌△DFH(AAS),
∴AG=DH,
在Rt△ABG和Rt△DEH中,
|
∴△ABG≌△DEH(HL),
∴∠B=∠E,
在△ABC和△DEF中,
|
∴△ABC≌△DEF(AAS).
点评:本题主要考查全等三角形的判定方法,掌握全等三角形的判定方法是解题的关键,即SSS、SAS、ASA、AAS和HL.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
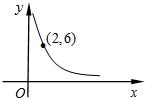 如图是反比例函数y=
如图是反比例函数y=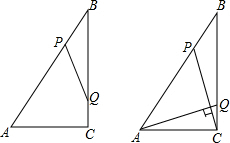 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点B出发,在BA边上以每秒5cm的速度向点A匀速运动,同时动点Q从点C出发,在CB边上以每秒4cm的速度向点B匀速运动,运动时间为t秒(0<t<2),连接PQ.