Question

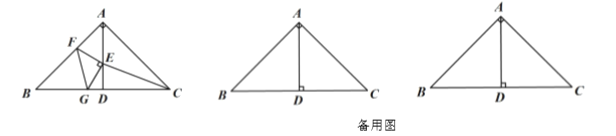
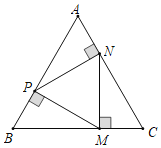
【题目】在△ABC中,AB=BC,∠B=90°,将△ABC沿BC方向平移,得到△A'CC',以C为位似中心,作△DEC与△ABC位似,位似比为1∶2,若F为CC'的中点,连接DF,A'F,则的值为_____.

Answer 1

【答案】1或

【解析】

设AB=BC=2x，①如图1，当点D在AC上时，根据平移的性质及中点的定义得出CF=x，继而可得A′F= = x，由位似图形的性质可得DE=CE=x、EF=2x，继而知DF==x，即可得 的值；②如图2，当点D在AC延长线上时,由①知A′F= =x，DF=DE=x，即可得的值．

解：设AB=BC=2x，
①如图1，当点D在AC上时，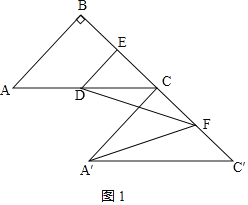

∵△ABC≌△A′CC′，
∴A′C=CC′=2x，
∵F为CC'的中点，
∴CF=x，
则A′F== x，
又∵△DEC∽△ABC，且 = =，
∴DE=CE=x，
则EF=2x，
∴DF==x，
∴ ==1；
②如图2，当点D在AC延长线上时，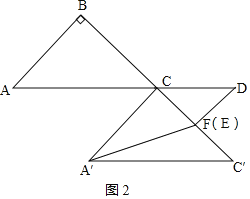

由①知A′F= =x，DF=DE=x，
∴ ==，
故答案为：1或．