题目内容
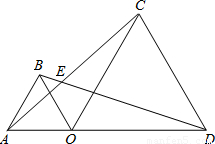
 已知点O为线段AD上一点,分别以AO、DO为边在线段的同侧作等边△OAB和等边△ODC,连接AC、BD相交于点E,求∠AEB的大小.
已知点O为线段AD上一点,分别以AO、DO为边在线段的同侧作等边△OAB和等边△ODC,连接AC、BD相交于点E,求∠AEB的大小.
解:∵等边△OAB和等边△ODC,
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中,
 ,
,
∴△AOC≌△BOD(SAS),
∴∠ACO=∠BDO,
又∠COD为△AOC的外角,
∴∠COD=∠CAO+∠ACO=∠CAO+∠BDO=60°,
又∠AEB为△AED的外角,
则∠AEB=∠CAO+∠BDO=60°.
分析:由三角形AOB与三角形COD都为等边三角形,利用等边三角形的性质得到AO=BO,OC=OD,且∠AOB=∠COD=60°,两边都加上∠BOC,得到一对角相等,利用SAS可得出三角形AOC与三角形BOD全等,由全等三角形的对应角相等得到∠ACO=∠BDO,由∠COD为三角形AOC的外角,利用外角性质得到∠COD=∠CAO+∠OCA=60°,等量代换可得出∠COD=∠CAO+∠ODB=60°,再由所求角为三角形AED的外角,利用外角性质即可求出角的度数.
点评:此题考查了全等三角形的判定与性质,等边三角形的性质,以及三角形的外角性质,熟练掌握全等三角形的判定与性质是解本题的关键.
∴OA=OB,OC=OD,∠AOB=∠COD=60°,
∴∠AOB+∠BOC=∠COD+∠BOC,即∠AOC=∠BOD,
在△AOC和△BOD中,
 ,
,∴△AOC≌△BOD(SAS),
∴∠ACO=∠BDO,
又∠COD为△AOC的外角,
∴∠COD=∠CAO+∠ACO=∠CAO+∠BDO=60°,
又∠AEB为△AED的外角,
则∠AEB=∠CAO+∠BDO=60°.
分析:由三角形AOB与三角形COD都为等边三角形,利用等边三角形的性质得到AO=BO,OC=OD,且∠AOB=∠COD=60°,两边都加上∠BOC,得到一对角相等,利用SAS可得出三角形AOC与三角形BOD全等,由全等三角形的对应角相等得到∠ACO=∠BDO,由∠COD为三角形AOC的外角,利用外角性质得到∠COD=∠CAO+∠OCA=60°,等量代换可得出∠COD=∠CAO+∠ODB=60°,再由所求角为三角形AED的外角,利用外角性质即可求出角的度数.
点评:此题考查了全等三角形的判定与性质,等边三角形的性质,以及三角形的外角性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
 已知点O为线段AD上一点,分别以AO、DO为边在线段的同侧作等边△OAB和等边△ODC,连接AC、BD相交于点E,求∠AEB的大小.
已知点O为线段AD上一点,分别以AO、DO为边在线段的同侧作等边△OAB和等边△ODC,连接AC、BD相交于点E,求∠AEB的大小.
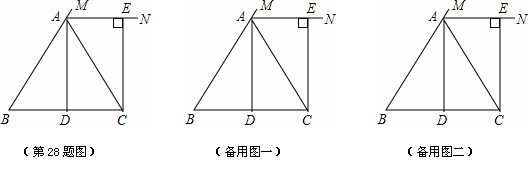 (3)已知有两个动点G,Q,其中G点在线段CE上运动,Q点在线段BD上运动,线段GQ的中点为R,求动点R所在区域的面积。
(3)已知有两个动点G,Q,其中G点在线段CE上运动,Q点在线段BD上运动,线段GQ的中点为R,求动点R所在区域的面积。