题目内容
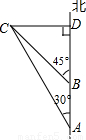
如图所示，一艘轮船以30海里/小时的速度向正北方向航行，在A处得灯塔C在北偏西30°方向，轮船航行2小时后到达B处，在B处时测得灯塔C在北偏西45°方向．当轮船到达灯塔C的正东方向的D处时，求此时轮船与灯塔C的距离．（结果精确到0.1海里，参考数据
≈1.41，
≈1.73）
【答案】分析：本题中CD是Rt△CDB和Rt△ADC的共有直角边，那么可用CD来表示出AD和BD，再根据AB的长来求出CD．
解答：解：设CD=x，
在Rt△BCD中，∠CBD=45°得BD=CD=x，
又∵AB=30×2=60，
∴AD=60+x，
在Rt△ACD中，
tan30°=
，
即
=
，
解得：x=30
+30，
得CD≈30×（1.73+1）=81.9（海里），
答：此时轮船与灯塔C的距离为81.9海里．
点评：此题考查的是解直角三角形的应用-方向角问题，两个直角三角形有公共的直角边时，利用好这条公共的直角边是解决此类问题的关键．
解答：解：设CD=x，
在Rt△BCD中，∠CBD=45°得BD=CD=x，
又∵AB=30×2=60，
∴AD=60+x，
在Rt△ACD中，
tan30°=
，即
=，解得：x=30
+30，得CD≈30×（1.73+1）=81.9（海里），
答：此时轮船与灯塔C的距离为81.9海里．
点评：此题考查的是解直角三角形的应用-方向角问题，两个直角三角形有公共的直角边时，利用好这条公共的直角边是解决此类问题的关键．
练习册系列答案
天天练口算系列答案
相关题目
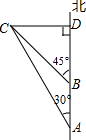如图所示，一艘轮船以30海里/小时的速度向正北方向航行，在A处得灯塔C在北偏西30°方向，轮船航行2小时后到达B处，在B处时测得灯塔C在北偏西45°方向．当轮船到达灯塔C的正东方向的D处时，求此时轮船与灯塔C的距离．
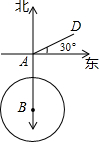（1998•河北）如图所示，一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，台风中心20
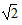≈1.41，
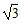≈1.73）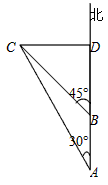 
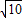海里的圆形区域（包括边界）都属台风区．当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里．
≈3.6）？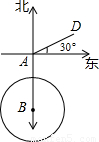
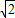≈1.41，
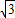≈1.73）