题目内容
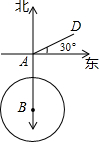 (1998•河北)如图所示,一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,台风中心20
(1998•河北)如图所示,一艘轮船以20海里/时的速度由西向东航行,途中接到台风警报,台风中心正以40海里/时的速度由南向北移动,台风中心20| 10 |
(1)若这艘轮船自A处按原速度继续航行,在途中会不会遇到台风?若会,试求轮船最初遇到台风的时间;若不会,请说明理由;
(2)现轮船自A处立即提高船速,向位于东偏北30°方向,相距60海里的D港驶去.为使台风到来之到达D港,问船速至少应提高多少(提高的船速取整,
| 13 |
分析:(1)设t时刻,轮船行驶到C点,台风中心运动到B点,列出轮船到台风中心的计算公式,求出即可,
(2)由于20
>60,则当B未到达A点时D已经受到影响,作出图形,根据勾股定理可以得出此时AB的距离,进而得出所用的时间,由AD的距离,则可以得出速度
(2)由于20
| 10 |
解答:解:(1)若这艘轮船自A处按原速继续航行,在途中会遇到台风.
设t时刻,轮船行驶到C点,台风中心运动到B点,如图所示:
则可知AC=20t,AB=100-40t,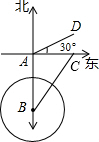
根据勾股定理得:BC=20
,
当BC=20
时,
整理得出:t2-4t+3=0
解得:t1=1,t2=3,
∵求最初遇台风时间,∴t=1,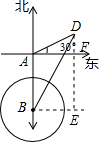
即点C在台风影响的范围内,会受到影响,轮船最初遇到台风的时间是行驶1小时.
(2)如图过点D作垂线,D位于东偏北30°,且AD=60,
则可以得出AF=BE=30
,DF=30,
有BD=20
,根据勾股定理得:DE2=BD2-BE2,
代入数据得:DE=10
,∴AB=EF=DE-DF=10
-30,
∴B点运动的距离为100-(10
-30),
∴用时间为
≈2.35,
∴轮船的速度为:
≈25.53,
∴船速至少应提高25.53-20≈6海里/时.
设t时刻,轮船行驶到C点,台风中心运动到B点,如图所示:
则可知AC=20t,AB=100-40t,

根据勾股定理得:BC=20
| 5t2-20t+25 |
当BC=20
| 10 |
整理得出:t2-4t+3=0
解得:t1=1,t2=3,
∵求最初遇台风时间,∴t=1,

即点C在台风影响的范围内,会受到影响,轮船最初遇到台风的时间是行驶1小时.
(2)如图过点D作垂线,D位于东偏北30°,且AD=60,
则可以得出AF=BE=30
| 3 |
有BD=20
| 10 |
代入数据得:DE=10
| 13 |
| 13 |
∴B点运动的距离为100-(10
| 13 |
∴用时间为
130-10
| ||
| 40 |
∴轮船的速度为:
| 60 |
| 2.35 |
∴船速至少应提高25.53-20≈6海里/时.
点评:本题考查了一元二次方程的应用和勾股定理的运用,对于这类问题要找到临界的点,运用所学的基本知识求解.这就要求对一些小的知识点有很好的掌握.

练习册系列答案
相关题目
 (1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( )
(1998•河北)已知:如图弦AB经过⊙O的半径OC的中点P,且AP=2,PB=3,则是⊙O的半径等于( ) (1998•河北)已知:如图,在⊙O中,直径AB⊥CD,BE切⊙O于B,且BE=BC,CE交AB于F、交⊙O于M,连接MO并延长,交⊙O于N.则下列结论中,正确的是( )
(1998•河北)已知:如图,在⊙O中,直径AB⊥CD,BE切⊙O于B,且BE=BC,CE交AB于F、交⊙O于M,连接MO并延长,交⊙O于N.则下列结论中,正确的是( ) (1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G.
(1998•河北)已知:如图△ABC中,∠A的平分线AD交BC于D,⊙O过点A,且与BC相切于D,与AB、AC分别相交于E、F,AD与EF相交于G.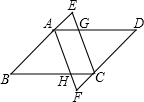 (1998•河北)已知:如图,四边形ABCD为平行四边形,延长BA到E,延长DC到F,使BE=DF,AF交BC于H,CE交AD于G.
(1998•河北)已知:如图,四边形ABCD为平行四边形,延长BA到E,延长DC到F,使BE=DF,AF交BC于H,CE交AD于G.