题目内容
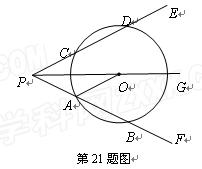
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与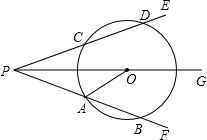 ∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.
∠EPF的两边相交于A、B和C、D,连接OA,此时有OA∥PE.(1)求证:AP=AO;
(2)若tan∠OPB=
| 1 | 2 |
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为
分析:(1)由已知条件“射线PG平分∠EPF”求得∠DPO=∠BPO;然后根据平行线的性质,两直线OA∥PE,内错角∠DPO=∠POA;最后由等量代换知∠BPO=∠POA,从而根据等角对等边证明AP=AO;
(2)设OH=x,则PH=2x.作辅助线OH(“过点O作OH⊥AB于点H”),根据垂径定理知AH=HB=
AB;又由已知条件“tan∠OPB=
”求得PH=2OH;然后利用(1)的结果及勾股定理列出关于x的一元二次方程,解方程即可;
(3)根据菱形的性质、等腰梯形的判定定理填空.
(2)设OH=x,则PH=2x.作辅助线OH(“过点O作OH⊥AB于点H”),根据垂径定理知AH=HB=
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据菱形的性质、等腰梯形的判定定理填空.
解答: (1)证明:∵PG平分∠EPF,
(1)证明:∵PG平分∠EPF,
∴∠DPO=∠BPO,
∵OA∥PE,
∴∠DPO=∠POA,
∴∠BPO=∠POA,
∴PA=OA;(2分)
(2)解:过点O作OH⊥AB于点H,则AH=HB=
AB,(1分)
∵tan∠OPB=
=
,∴PH=2OH,(1分)
设OH=x,则PH=2x,
由(1)可知PA=OA=10,∴AH=PH-PA=2x-10,
∵AH2+OH2=OA2,∴(2x-10)2+x2=102,(1分)
解得x1=0(不合题意,舍去),x2=8,
∴AH=6,∴AB=2AH=12;(1分)
(3)解:P、A、O、C;A、B、D、C或P、A、O、D或P、C、O、B.(2分)
(写对1个、2个、3个得(1分),写对4个得2分)
 (1)证明:∵PG平分∠EPF,
(1)证明:∵PG平分∠EPF,∴∠DPO=∠BPO,
∵OA∥PE,
∴∠DPO=∠POA,
∴∠BPO=∠POA,
∴PA=OA;(2分)
(2)解:过点O作OH⊥AB于点H,则AH=HB=
| 1 |
| 2 |
∵tan∠OPB=
| OH |
| PH |
| 1 |
| 2 |
设OH=x,则PH=2x,
由(1)可知PA=OA=10,∴AH=PH-PA=2x-10,
∵AH2+OH2=OA2,∴(2x-10)2+x2=102,(1分)
解得x1=0(不合题意,舍去),x2=8,
∴AH=6,∴AB=2AH=12;(1分)
(3)解:P、A、O、C;A、B、D、C或P、A、O、D或P、C、O、B.(2分)
(写对1个、2个、3个得(1分),写对4个得2分)
点评:本题综合考查了垂径定理、勾股定理、菱形的性质、等腰梯形的判定定理及锐角三角函数的定义.解此类题目要注意将圆的问题转化成三角形的问题再进行计算.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
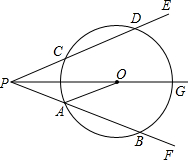 如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心作⊙O,分别与∠EPF两边相交于A、B和C、D,连接OA,此时有OA∥PE.
如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心作⊙O,分别与∠EPF两边相交于A、B和C、D,连接OA,此时有OA∥PE. ,求弦AB的长;
,求弦AB的长;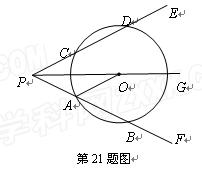
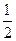 ,求弦AB的长;
,求弦AB的长;