题目内容
(本题8分)如图,射线PG平分∠EPF,O为射线PG上一点,以O为圆心,10为半径作⊙O,分别与∠EPF 的两边相交于A、B和C、D,连结OA,此时有OA//PE.
(1)求证:AP=AO;
(2)若tan∠OPB=![]() ,求弦AB的长;
,求弦AB的长;
(3)若以图中已标明的点(即P、A、B、C、D、O)构造四边形,则能构成菱形的四个点为 ▲ ,能构成等腰梯形的四个点为 ▲ 或 ▲ 或 ▲ .
(本题8分)
(1)∵PG平分∠EPF,
∴∠DPO=∠BPO ,
∵OA//PE,
∴∠DPO=∠POA ,
∴∠BPO=∠POA,
∴PA=OA; ……2分
(2)过点O作OH⊥AB于点H,则AH=HB=![]() AB,……1分
AB,……1分
∵ tan∠OPB=![]() ,∴PH=2OH, ……1分
,∴PH=2OH, ……1分
设OH=![]() ,则PH=2
,则PH=2![]() ,
,
由(1)可知PA=OA=10 ,∴AH=PH-PA=2![]() -10,
-10,
∵![]() , ∴
, ∴![]() , ……1分
, ……1分
解得![]() (不合题意,舍去),
(不合题意,舍去),![]() ,
,
∴AH=6, ∴AB=2AH=12; ……1分
(3)P、A、O、C;A、B、D、C或 P、A、O、D或P、C、O、B.……2分(写对1个、2个、3个得1分,写对4个得2分)
解析:略

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
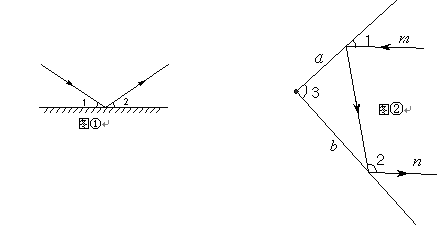

 射到平面镜
射到平面镜 上,被
上,被 上,又被
上,又被 与光线
与光线

 射到平面镜
射到平面镜 上,被
上,被 上,又被
上,又被 与光线
与光线