题目内容
 如图,已知DC=1,AB=3,∠ABC与∠DAB互余,则BD2+AC2的值为( )
如图,已知DC=1,AB=3,∠ABC与∠DAB互余,则BD2+AC2的值为( )分析:如图,分别延长AD、BC交于点E.构建直角△AEB.在直角△ACE与直角△BDE中,利用勾股定理求得AC2+BD2=(AE2+BE2)+(CE2+DE2)=AB2+DC2=32+12=10.
解答:解:如图,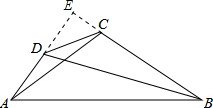 分别延长AD、BC交于点E.
分别延长AD、BC交于点E.
∵∠ABC与∠DAB互余,
∴∠AEB=90°,
∴AC2+BD2
=AE2+CE2+BE2+DE2
=(AE2+BE2)+(CE2+DE2)
=AB2+DC2
=32+12
=10.
故选A.
 分别延长AD、BC交于点E.
分别延长AD、BC交于点E.∵∠ABC与∠DAB互余,
∴∠AEB=90°,
∴AC2+BD2
=AE2+CE2+BE2+DE2
=(AE2+BE2)+(CE2+DE2)
=AB2+DC2
=32+12
=10.
故选A.
点评:本题考查了勾股定理.勾股定理应用的前提条件是在直角三角形中.

练习册系列答案
相关题目
 如图,已知DC⊥AC,DB⊥AB,点C,B为垂足,AC=AB,AD与BC相交于点O.
如图,已知DC⊥AC,DB⊥AB,点C,B为垂足,AC=AB,AD与BC相交于点O.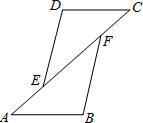 如图,已知DC∥AB,DC=AB,AE=CF,求证:DE=BF.
如图,已知DC∥AB,DC=AB,AE=CF,求证:DE=BF. 如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是( )
如图,已知DC∥EF,点A在DC上,BA的延长线交EF于点G,AB=AC,∠AGE=130°,则∠B的度数是( ) 如图,已知DC是△ABC中∠ACB的外角平分线,是否可以判定∠BAC与∠B的大小?若能够判定说明理由,不能判定也说明理由.
如图,已知DC是△ABC中∠ACB的外角平分线,是否可以判定∠BAC与∠B的大小?若能够判定说明理由,不能判定也说明理由.