题目内容
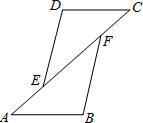如图，已知DC∥AB，DC=AB，AE=CF，求证：DE=BF．分析：首先根据平行线的性质可得∠C=∠A，再根据AE=CF可证出AF=CE，再加上条件DC=AB可利用SAS证明△DCE≌△BAF，然后根据全等三角形对应边相等可得DE=BF．
解答：证明：∵DC∥AB，
∴∠C=∠A，
∵AE=CF，
∴AE+EF=CF+EF，
即：AF=CE，
在△DCE和△BAF中，
，
∴△DCE≌△BAF（SAS），
∴DE=BF．
∴∠C=∠A，
∵AE=CF，
∴AE+EF=CF+EF，
即：AF=CE，
在△DCE和△BAF中，
|
∴△DCE≌△BAF（SAS），
∴DE=BF．
点评：此题主要考查了全等三角形全等的判定与性质，关键是掌握证明三角形全等的判定方法SSS、SAS、AAS、ASA．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
如图，已知线段AB=6，BC=2AB，点D是AC的中点，则DC的长等于
AB，E为AB的中点。
。
外，还有与
的面积相等的三角形吗？若有请写写。
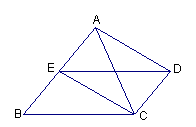
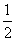AB，E为AB的中点。