题目内容
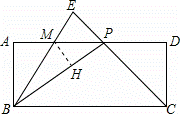
已知在矩形ABCD中,P是边AD上的一动点,联结BP、CP,过点B作射线交线段CP的延长线于点E,交边AD于点M,且使得∠ABE=∠CBP,如果AB=2,BC=5,AP=x,PM=y;
(1)求y关于x的函数解析式,并写出 它的定义域;
它的定义域;
(2)当AP=4时,求∠EBP的正切值;
(3)如果△EBC是以∠EBC为底角的等腰三角形,求AP的长.
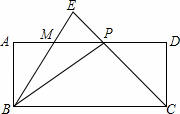
解:(1)∵四边形ABCD是矩形,
∴AB=CD=2,AD=BC=5,∠A=∠D=90°,AD∥BC,
∴∠APB=∠PBC.
∵∠ABE=∠CBP,
∴∠ABM=∠APB.
又∵∠A=∠A,
∴△ABM∽△APB,
∴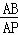 =
=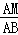 ,
,
∴ =
=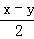 ,
,
∴y=x﹣ .
.
∵P是边AD上的一动点,
∴0≤x≤5.
∵y>0,
∴x﹣ >0,
>0,
∴x>2,
∴函数的定义域为2<x≤5;
(2)过点M作MH⊥BP于H,如图.
∵AP=x=4,∴y=x﹣ =3,
=3,
∴MP=3,AM=1,
∴BM=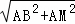 =
=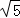 ,BP=
,BP=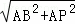 =2
=2 .
.
∵S△BMP=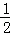 MP•AB=
MP•AB=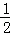 BP•MH,
BP•MH,
∴MH=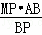 =
=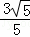 ,
,
∴BH= =
= ,
,
∴tan∠EBP= =
=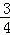 ;
;
(3)①若EB=EC,
则有∠EBC=∠ECB.
∵AD∥BC,
∴∠AMB=∠EBC,∠DPC=∠ECB,
∴∠AMB=∠DPC.
在△AMB和△DPC中,
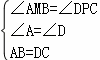 ,
,
∴△AMB≌△DPC,
∴AM=DP,
∴x﹣y=5﹣x,
∴y=2x﹣5,
∴x﹣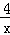 =2x﹣5,
=2x﹣5,
解得:x1=1,x2=4.
∵2<x≤5,
∴AP=x=4;
②若CE=CB,
则∠EBC=∠E.
∵AD∥BC,
∴∠EMP=∠EBC=∠E,
∴PE=PM=y,
∴PC=EC﹣EP=5﹣y,
∴在Rt△DPC中,
(5﹣y)2﹣(5﹣x)2=22,
∴(10﹣x﹣y)(x﹣y)=4,
∴(10﹣x﹣x+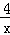 )(x﹣x+
)(x﹣x+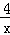 )=4,
)=4,
整理得:3x2﹣10x﹣4=0,
解得:x3=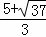 ,x4=
,x4=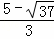 (舍负).
(舍负).
∴AP=x=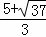 .
.
终上所述:AP的值为4或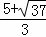 .
.

 发散思维新课堂系列答案
发散思维新课堂系列答案 月份A款汽车每辆售价多少万元?
月份A款汽车每辆售价多少万元?
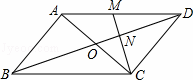

 ,PF之间存在什么关系?并说明理由.
,PF之间存在什么关系?并说明理由.
