题目内容
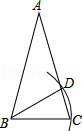
如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线点F.问:
(1)图中△APD与哪个三角形全等?并说明理由;
(2)求证:△APE∽△FPA;
(3)猜想:线段PC,PE ,PF之间存在什么关系?并说明理由.
,PF之间存在什么关系?并说明理由.

解:(1)△APD≌△CPD.
理由:∵四边形ABCD是菱形,
∴AD=CD,∠ADP=∠CDP.
又∵PD=PD,
∴△APD≌△CPD.
证明:(2)∵△APD≌△CPD,
∴∠DAP=∠DCP,
∵CD∥AB,
∴∠DCF=∠DAP=∠CFB,
又∵∠FPA=∠FPA,
∴△APE∽△FPA.
猜想:(3)PC2=PE•PF.
理由:∵△APE∽△FPA,
∴ .
.
∴PA2=PE•PF.
∵△APD≌△CPD,
∴PA=PC.
∴PC2=PE•PF.


练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
 它的定义域;
它的定义域;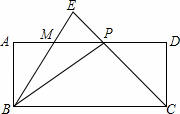

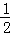 S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
S四边形AEOF?若存在,请求出此时t的值;若不存在,请说明理由.
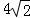 ,则a的值是( )
,则a的值是( )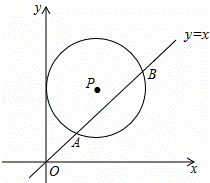
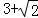 C.
C.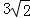 D.
D. 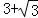


 ,求sinB+cosB的值.
,求sinB+cosB的值.