Question

14．如图，在边长为6的正方形ABCD中，点E为AD边上的一个动点（与点A、D不重合），∠EBM=45°，BE交对角线AC于点F，BM交对角线AC于点G，交CD于点M．
（1）如图1，联结BD，求证：△DEB∽△CGB，并写出DE：CG的值；
（2）联结EG，如图2，若设AE=x，EG=y，求y关于x的函数解析式，并写出函数的定义域；
（3）当M为边DC的三等分点时，求S_△EGF的面积．

Answer 1

分析 （1）根据正方形的性质得到∠EDB=∠GCB=45°，∠ABD=∠CBD=45°，根据相似三角形的判定定理证明即可；
（2）作EH⊥AC于H，根据等腰直角三角形的性质、勾股定理和相似三角形的性质得到y关于x的函数解析式；
（3）分CM=$\frac{1}{3}$CD和CM=$\frac{2}{3}$CD两种情况，根据相似三角形的性质解答即可．

解答 （1）证明：∵四边形ABCD是正方形，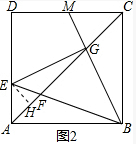
∴∠EDB=∠GCB=45°，∠ABD=∠CBD=45°，又∠EBM=45°，
∴∠GBC+∠DBM=45°，∠EBD+∠DBM=45°，
∴∠GBC=∠EBD，又∠EDB=∠GCB=45°，
∴△DEB∽△CGB，
∴DE：CG=BD：BC=$\sqrt{2}$；
（2）如图2，作EH⊥AC于H，
则AH=EH=$\frac{\sqrt{2}}{2}$x，
∵△DEB∽△CGB，
∴$\frac{CG}{DE}$=$\frac{BC}{BD}$=$\frac{\sqrt{2}}{2}$，
∴CG=$\frac{\sqrt{2}}{2}$（6-x），
∴HG=AC-AH-CG=3$\sqrt{2}$，
∵EG²=EH²+HG²，
∴y=$\frac{\sqrt{2{x}^{2}+72}}{2}$（0＜x＜6）；
（3）当CM=$\frac{1}{3}$CD=2时，
∵四边形ABCD是正方形，
∴CD∥AB，
∴$\frac{CM}{AB}$=$\frac{CG}{AG}$=$\frac{1}{3}$，
∴CG=$\frac{3}{2}\sqrt{2}$，
∴DE=3，则AE=3，
∴AH=EH=$\frac{3}{2}\sqrt{2}$，
∵AD∥BC，
∴$\frac{AE}{BC}$=$\frac{AF}{CF}$=$\frac{1}{2}$，
∴AF=2$\sqrt{2}$，
∴GF=AC-AF-CG=$\frac{5}{2}$$\sqrt{2}$，
∴S_△EGF=$\frac{1}{2}$×FG×EH=$\frac{15}{4}$，
当CM=$\frac{2}{3}$CD=4时，
$\frac{CM}{AB}$=$\frac{CG}{AG}$=$\frac{2}{3}$，
∴CG=$\frac{12}{5}$$\sqrt{2}$，
∴DE=$\frac{24}{5}$，则AE=$\frac{6}{5}$，
AH=EH=$\frac{3\sqrt{2}}{5}$，
∵$\frac{AE}{BC}=\frac{AF}{CF}=\frac{1}{5}$，
∴AF=$\sqrt{2}$，
∴GF=AC-AF-CG=$\frac{13\sqrt{2}}{5}$，
∴S_△EGF=$\frac{1}{2}$×FG×EH=$\frac{39}{25}$．

点评 本题考查的是相似三角形的判定和性质的应用、正方形的性质的应用，正确作出辅助线、灵活运用相关的定理是解题的关键，注意分情况讨论思想的运用．