题目内容
15. 如图,在Rt△AED中,∠E=90°,AE=6,cosA=$\frac{3}{5}$,求AD、ED、sin∠D、cos∠D、tan∠D的值.
如图,在Rt△AED中,∠E=90°,AE=6,cosA=$\frac{3}{5}$,求AD、ED、sin∠D、cos∠D、tan∠D的值.
分析 首先利用锐角三角函数关系得出AD的长,再利用勾股定理得出DE的长,进而分别得出sin∠D、cos∠D、tan∠D的值.
解答 解:∵∠E=90°,AE=6,cosA=$\frac{3}{5}$,
∴cosA=$\frac{AE}{AD}$=$\frac{3}{5}$=$\frac{6}{AD}$,
解得:AD=10,
则DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=8,
故sin∠D=$\frac{AE}{AD}$=$\frac{6}{10}$=$\frac{3}{5}$、cos∠D=$\frac{DE}{AD}$=$\frac{8}{10}$=$\frac{4}{5}$、tan∠D=$\frac{AE}{DE}$=$\frac{6}{8}$=$\frac{3}{4}$.
点评 此题主要考查了解直角三角形,正确记忆各锐角三角函数关系是解题关键.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
7.下列事件是随机事件的是( )
| A. | 在一个标准大气压下,加热到100℃,水沸腾 | |
| B. | 购买一张福利彩票,中奖 | |
| C. | -2的绝对值小于0 | |
| D. | 在一个仅装着白球和黑球的袋中摸球,摸出红球 |

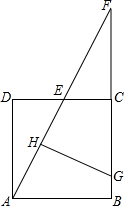 如图,ABCD是边长为a的正方形,E是CD中点,AE和BC的延长线相交于点F,AE的垂直平分线交AE、BC于H、G,求线段FG的长.
如图,ABCD是边长为a的正方形,E是CD中点,AE和BC的延长线相交于点F,AE的垂直平分线交AE、BC于H、G,求线段FG的长.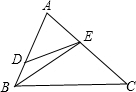 如图,在△ABC中,∠C=45°=∠ADE,BC•AE=24,则S△ABE=6$\sqrt{2}$.
如图,在△ABC中,∠C=45°=∠ADE,BC•AE=24,则S△ABE=6$\sqrt{2}$.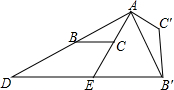 如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.
如图,△ABC中,AC=2,把△ABC绕点A逆时针旋转90°得到△AB′C′,过点B′作BC的平行线,分别交AB、AC的延长线于D、E两点,∠AED=120°,EB′=2$\sqrt{3}$,AB的长为2$\sqrt{3}$.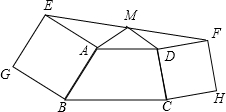 梯形ABCD中,AD∥BC,分别从两腰AB、CD为边作正方形ABGE和CDFH.M为EF中点,求证:MA=MD.
梯形ABCD中,AD∥BC,分别从两腰AB、CD为边作正方形ABGE和CDFH.M为EF中点,求证:MA=MD.