题目内容
若ab=0,则P点(a,b)在( )
| A、x轴上 | B、y轴上 |
| C、坐标原点上 | D、x轴或y轴上 |
考点:点的坐标
专题:
分析:由ab=0则得a=0,b=0或a≠0,b=0或a=0,b≠0即可求得P点(a,b)所在位置.
解答:解:∵ab=0,
∴可得到a=0,b=0即为原点或a≠0,b=0即为横轴上的一点或a=0,b≠0纵轴上的一点,
∴P点(a,b)在x轴或y轴上.
故选D.
∴可得到a=0,b=0即为原点或a≠0,b=0即为横轴上的一点或a=0,b≠0纵轴上的一点,
∴P点(a,b)在x轴或y轴上.
故选D.
点评:本题考查了坐标轴上点的坐标特征,熟记x轴上的点纵坐标为0,y轴上的点横坐标为0是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
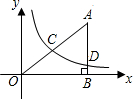 在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=
在直角坐标系中,有如图所示的Rt△ABO,AB⊥x轴于点B,斜边AO=10,sin∠AOB=| 3 |
| 5 |
| k |
| x |
A、(8,
| ||
B、(6,
| ||
C、(
| ||
D、(8,
|
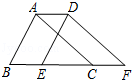 如图,将周长为7的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )
如图,将周长为7的△ABC沿BC方向平移1个单位得到△DEF,则四边形ABFD的周长为( )| A、8 | B、9 | C、10 | D、11 |
为了确保信息安全,信息需要加密传输,发送方将明文加密传输给接收方,接收方收到密文后解密还原为明文,已知某种加密规则为:明文a、b对应的密文为a-2b、2a+b,例如1、2对应的密文为-3、4,当接收方收到的密文是1、12时,那么解密得到明文是( )
| A、-1、1 | B、5、2 |
| C、2、5 | D、1、1 |
下列各式中能用平方差公式分解的是( )
| A、x2+4y2 |
| B、-x2-4y2 |
| C、x2-2y2+1 |
| D、x2-4y2 |