题目内容
11.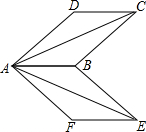 如图,平行四边形ABCD与平行四边形ABEF有公共边AB,且∠D=∠F,BC=BE,连接AC、AE.
如图,平行四边形ABCD与平行四边形ABEF有公共边AB,且∠D=∠F,BC=BE,连接AC、AE.(1)试说明AC=AE;
(2)连接CE、DF,猜想四边形CDFE的形状,并说明理由.
分析 (1)根据平行四边形的性质得出∠D=∠ABC,∠F=∠ABE,求出∠ABC=∠ABE,根据全等三角形的判定得出即可;
(2)先根据平行四边形的性质得出DC∥EF,DC=EF,根据平行四边形的判定推出四边形CDFE是平行四边形,再求出∠DCE=90°,根据矩形的判定推出即可.
解答 解:(1)∵平行四边形ABCD与平行四边形ABEF有公共边AB,
∴∠D=∠ABC,∠F=∠ABE,
∵∠D=∠F,
∴∠ABC=∠ABE,
在△ABC和△ABE中
$\left\{\begin{array}{l}{AB=AB}\\{∠ABC=∠ABE}\\{BC=BE}\end{array}\right.$
∴△ABC≌△ABE,
∴AC=AE;
(2)四边形CDFE是矩形,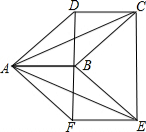
理由是:∵四边形ABCD和四边形ABEπF是平行四边形,BC=BE,
∴AD=AF,DC=AB=EF,DC∥AB∥EF,
∴CDFE是平行四边形,
在△ADC和△AFE中,
$\left\{\begin{array}{l}{DC=EF}\\{AD=AF}\\{AC=AE}\end{array}\right.$,
∴△ADC≌△AFE,
∴∠DCA=∠FEA,
∵AC=AE,
∴∠ACE=∠AEC,
∴∠DCE=∠FEC,
∵DC∥BF,
∴∠DCE+∠FEC=180°,
∴∠DCE=90°,
∴四边形CDFE是矩形.
点评 本题考查了平行四边形的性质和判定,平行线的性质,等腰三角形的性质和判定,全等三角形的性质和判定的应用,能综合运用定理进行推理是解此题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
1.月亮岛是鸭绿江上一个面积为13.4万平方米的美丽小岛,就如一叶轻舟与以抗美援朝而著名的鸭绿江大桥遥相辉映.数据13.4万用科学记数法表示为( )
| A. | 1.34×104 | B. | 13.4×104 | C. | 1.34×105 | D. | 0.134×106 |
2.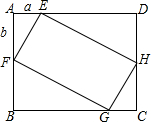 如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
 如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )
如图,在矩形ABCD中,AB=4,BC=5,点E、F、G、H分别在已知矩形的四条边上,且四边形EFGH也是矩形,GF=2EF.若设AE=a,AF=b,则a与b满足的关系为( )| A. | $\left\{\begin{array}{l}{a+b=4}\\{a+2b=5}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{2a+b=4}\\{a+2b=5}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=2b}\\{2a+b=5}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{2a+b=5}\\{a+2b=4}\end{array}\right.$ |
19.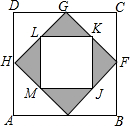 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )
如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )
 如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )
如图,顺次连接正方形ABCD各边的中点得到四边形EFGH,顺次连接四边形EFGH各边的中点得到四边形JKLM,若向正方形ABCD中随机撒一粒豆子,则它落在阴影部分的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
3.观察下列各数:1,$\frac{4}{3}$,$\frac{9}{7}$,$\frac{16}{15}$,…,按你发现的规律计算这列数的第6个数为( )
| A. | $\frac{25}{31}$ | B. | $\frac{36}{35}$ | C. | $\frac{4}{7}$ | D. | $\frac{62}{63}$ |
1.一个正常人的心跳平均每分70次,一天大约跳100800次,将100800用科学记数法表示为( )
| A. | 0.1008×106 | B. | 1.008×106 | C. | 1.008×105 | D. | 10.08×104 |
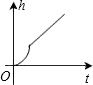
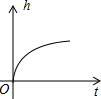
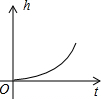
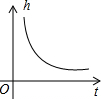
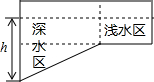 某游泳池横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反应深水区水深h与注水时间t关系的是( )
某游泳池横截面如图所示,用一水管向池内持续注水,若单位时间内注入的水量保持不变,则在注水过程中,下列图象能反应深水区水深h与注水时间t关系的是( )