Question

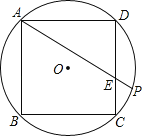
【题目】如图，正方形ABCD内接于⊙O，点P是上一动点，连接AP交CD于点E，则的最大值是_____．

Answer 1

【答案】

【解析】

过P作PQ⊥CD于Q，根据正方形的性质得到∠ADC＝90°，根据相似三角形的性质得到＝，于是得到取最大值时，即取最大值，由于AD一定，得到当PQ取最大值时，的值最大，推出当P为的中点时，PQ 最大，延长PQ交⊙O于另一点于M，则PM为⊙O的直径，设正方形的边长为a，则PM＝AC＝a，于是得到结论．

过P作PQ⊥CD于Q，

∵四边形ABCD是正方形，

∴∠ADC＝90°，

∴AD∥PQ，

∴△ADE∽△PQE，

∴＝，

∴取最大值时，即取最大值，

∵AD一定，

∴当PQ取最大值时，的值最大，

∴当P为的中点时，PQ 最大，

延长PQ交⊙O于另一点于M，

则PM为⊙O的直径，

设正方形的边长为a，则PM＝AC＝a，

∴PQ＝，

∴的最大值＝＝，

故答案为：．