Question

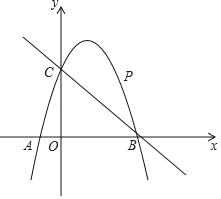
【题目】已知二次函数y＝ax2﹣（3a+1）x+2a+1（a≠0），与x轴交与A（x1，0）B（x2，0）两点，与y轴交与C点．

（1）求出该函数的图象经过的定点的坐标．

（2）若A为（1）中所求的某一定点，且x1、x2，之间的整数恰有3个（不包括x1、x2），试求a的取值范围．

（3）当a＝时，将与x轴重合的直线绕着D（﹣5，0）逆时针旋转得到直线l：y＝kx+b，过点C、B分别作l的垂线段，距离为d1、d2，试分别求出当|d1﹣d2|最大和最小时b的值．

Answer 1

【答案】（1）定点的坐标为（1，0）或（2，﹣1）；（2）﹣＜a≤﹣或≤a＜；（3）b的值为或﹣或10或或﹣10或．

【解析】

（1）由y＝ax2﹣（3a+1）x+2a+1 （a≠0），可得y＝（x2﹣3x+2）a﹣x+1，由该函数的图象经过的定点，可得x2﹣3x+2＝0，解方程即可解决问题；

（2）分两种情形讨论求解，分别列出不等式组即可解决问题；

（3）当B（4，0）时，①如图1中，CE⊥l于E，BF⊥l于F，连接BC交EF于K．当CE＝BF时，|d1﹣d2|的值最小，易证明△CEK≌△BFK，可得CK＝BK，推出K（2，1），求出直线DK的解析式即可解决问题；另外当直线平行BC时，|d1﹣d2|的值最小；②如图2中，如图2中，作 CK⊥BF于K，则四边形CEFK是矩形，在Rt△CBK中，易知BK≤BC，推出当BC⊥DE时，|d1﹣d2|的值最大，由此求出直线DE的解析式即可解决问题；当点B坐标为（1，0）时，同法可求；

（1）∵y＝ax2﹣（3a+1）x+2a+1 （a≠0），

∴y＝（x2﹣3x+2）a﹣x+1，

∵该函数的图象经过的定点，

∴x2﹣3x+2＝0，

∴x＝1或2，

∵x＝1时，y＝0，x＝2时，y＝﹣1，

∴定点的坐标为（1，0）或（2，﹣1）．

（2）易知A（1，0），B（2+ ，0），

∵x1、x2，之间的整数恰有3个（不包括x1、x2），

∴﹣3≤2+ ＜﹣2或4＜2+ ≤5，

解得﹣＜a≤﹣或≤a＜．

（3）∵a＝，

∴C（0，2），B（1，0）或（4，0），

①当B（4，0）时，①如图1中，CE⊥l于E，BF⊥l于F，连接BC交EF于K．

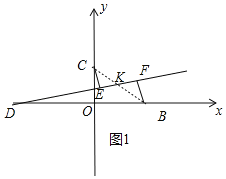
当CE＝BF时，|d1﹣d2|的值最小，易证明△CEK≌△BFK，

∴CK＝BK，

∵C（0，2），B（4，0），

∴K（2，1），

设直线l的解析式为y＝kx+b，

把D（﹣5，0），K（2，1）代入得到，

解得，

当直线与BC平行时，|d1﹣d2|的值最小，

∵直线BC的解析式为y＝﹣x+2，

此时直线的解析式为y＝﹣x﹣，

∴b＝﹣，

②如图2中，如图2中，作 CK⊥BF于K，则四边形CEFK是矩形，

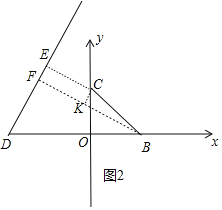
∵CE＝FK，

∴|d1﹣d2|＝BF﹣CE＝BK，

在Rt△CBK中，易知BK≤BC，

∴当BC⊥DE时，|d1﹣d2|的值最大，

∵直线BC的解析式为y＝﹣x+2，

∴可以假设直线DE的解析式为y＝2x+b，把D（﹣5，0）代入得到b＝10，

综上所述，满足条件的b的值为或﹣或10．

当B点坐标为（1，0）时，同法可求b的值为或﹣10或．