题目内容
 如图,已知△ABC是等边三角形,D、E分别为BC、AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q,PQ=3,则BP的长为
如图,已知△ABC是等边三角形,D、E分别为BC、AC上的点,且CD=AE,AD、BE相交于点P,BQ⊥AD于点Q,PQ=3,则BP的长为考点:全等三角形的判定与性质,含30度角的直角三角形
专题:
分析:易证∠CAB=∠C=60°,即可证明△ACD≌△BAE,可得∠AEB=∠ADC,即可求得∠APE=∠C=60°,可得∠PBQ=30°,根据30°角所对直角边是斜边一半的性质即可解题.
解答:解:∵△ABC是等边三角形,
∴∠CAB=∠C=60°,
在△ACD和△BAE中,
,
∴△ACD≌△BAE(SAS),
∴∠AEB=∠ADC,
∵∠C+∠ADC+∠CAD=180°,∠APE+∠AEB+∠CAD=180°,
∴∠APE=∠C=60°,
∴∠BPQ=60°,
∵BQ⊥AD,
∴∠PBQ=30°,
∴BP=2PQ=6.
∴∠CAB=∠C=60°,
在△ACD和△BAE中,
|
∴△ACD≌△BAE(SAS),
∴∠AEB=∠ADC,
∵∠C+∠ADC+∠CAD=180°,∠APE+∠AEB+∠CAD=180°,
∴∠APE=∠C=60°,
∴∠BPQ=60°,
∵BQ⊥AD,
∴∠PBQ=30°,
∴BP=2PQ=6.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证△ACD≌△BAE是解题的关键.

练习册系列答案
相关题目
用两个钉子把直木条钉在墙上,木条就固定了,这说明( )
| A、一条直线上只有两点 |
| B、两点确定一条直线 |
| C、过一点可画无数条直线 |
| D、直线可向两端无限延伸 |
 如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,则下列结论中,正确的是( )
如图,在△ABC中,∠ABC=50°,∠ACB=60°,点E在BC的延长线上,∠ABC的平分线BD与∠ACE的平分线CD相交于点D,连接AD,则下列结论中,正确的是( )| A、∠BAC=60° |
| B、∠DOC=85° |
| C、BC=CD |
| D、AC=AB |
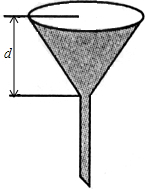 如图,某玻璃器皿制造公司要制造一种容积为1L(1L=1dm3)的圆锥形漏斗.
如图,某玻璃器皿制造公司要制造一种容积为1L(1L=1dm3)的圆锥形漏斗. 如图,BC为⊙O的直径,P为⊙O上一点,A为⊙O外的一点,AB,AC分别交⊙O于D,E,连接PE,PD,若∠P=28°,则∠A=
如图,BC为⊙O的直径,P为⊙O上一点,A为⊙O外的一点,AB,AC分别交⊙O于D,E,连接PE,PD,若∠P=28°,则∠A=