题目内容
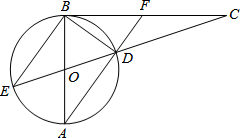
 如图,AB与⊙O相切于点C,OA=OB,⊙O直径为2cm,∠AOB=120°,则AB的长为
如图,AB与⊙O相切于点C,OA=OB,⊙O直径为2cm,∠AOB=120°,则AB的长为考点:切线的性质
专题:
分析:首先连接OC,由切线的性质,可得OC⊥AB,又由等腰三角形的性质,可得AC=BC,∠A=30°,继而求得答案.
解答: 解:连接OC,
解:连接OC,
∵AB与⊙O相切于点C,
∴OC⊥AB,
∵OA=OB,∠AOB=120°,
∴AC=BC=
AB,∠A=30°,
∵⊙O直径为2cm,
∴OC=1cm,
∴AC=
=
(cm),
∴AB=2
(cm).
故答案为:2
.
 解:连接OC,
解:连接OC,∵AB与⊙O相切于点C,
∴OC⊥AB,
∵OA=OB,∠AOB=120°,
∴AC=BC=
| 1 |
| 2 |
∵⊙O直径为2cm,
∴OC=1cm,
∴AC=
| OC |
| tta30° |
| 3 |
∴AB=2
| 3 |
故答案为:2
| 3 |
点评:此题考查了切线的性质以及等腰三角形的性质.此题难度不大,注意掌握辅助线的作法,注意数形结合思想的应用.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
 如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长,交⊙O于点D、E,连接AD并延长,交BC于点F.
如图,AB是⊙O的直径,BC切⊙O于点B,连接CO并延长,交⊙O于点D、E,连接AD并延长,交BC于点F. 如图,△ABC的面积为24,AD是BC边上的中线,E在AD上,且AE:ED=1:2,BE的延长线交AC于点F.则△AEF的面积为
如图,△ABC的面积为24,AD是BC边上的中线,E在AD上,且AE:ED=1:2,BE的延长线交AC于点F.则△AEF的面积为 网上销售已成为产品销售的一种重要方式,很多大学生也在网上开起了网店,某手机销售网店正在代理销售一种新型智能手机,手机每部进价为1000元,经过试销发现:售价x(元/部)与每天交易量y(部)之间满足如图所示关系.
网上销售已成为产品销售的一种重要方式,很多大学生也在网上开起了网店,某手机销售网店正在代理销售一种新型智能手机,手机每部进价为1000元,经过试销发现:售价x(元/部)与每天交易量y(部)之间满足如图所示关系.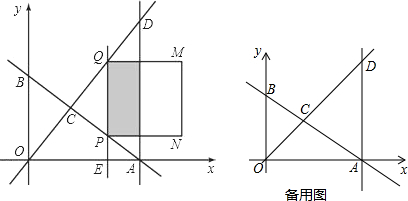
 如图,△ABC中,AB=AC,∠BA0=45°,△ABC内接于⊙0,D为⊙O上一点,过点D作⊙O的切线交BC的延长线于E,若DE⊥BC,AD=2
如图,△ABC中,AB=AC,∠BA0=45°,△ABC内接于⊙0,D为⊙O上一点,过点D作⊙O的切线交BC的延长线于E,若DE⊥BC,AD=2 如图,AD是△ABC的中线,过DC上任意一点F,作EG∥AB,与AC和AD的延长线分别交于G和E,FH∥AC交AB于点H
如图,AD是△ABC的中线,过DC上任意一点F,作EG∥AB,与AC和AD的延长线分别交于G和E,FH∥AC交AB于点H