Question

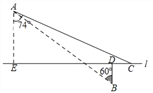
【题目】如图，△ABC 的面积为 63，D 是 BC 上的一点，且 BD：BC＝2：3， DE∥AC 交 AB 于点 E，延长 DE 到 F，使 FE：ED＝2：1．连结 CF 交 AB 点于 G．

(1)求△BDE 的面积；

(2)求 的值；

(3)求△ACG 的面积．

Answer 1

【答案】（1）△BDE的面积是28；（2）；（3）9

【解析】

（1）因为DE∥AC，所以△BDE∽△BCA，由相似三角形的性质：面积比等于相似比的平方可得到△BDE的面积；

（2）若要求 的值，可由相似三角形的性质分别得到AC和DE的数量关系、EF和DE的数量关系即可；

（3）由（1）可知△BDE的面积是28，因为BD：BC=2：3，所以BD：CD=2：1，又因为三角形BDE和三角形CDE中BD和CD边上的高相等，所以S =14，进而求出四边形ACDE的面积是35和S =21，利用相似三角

(1)∵DE∥AC，

∴△BDE∽△BCA，

∴ ，

∵BD:BC=2:3，

∴ ，

∵△ABC的面积为63，

∴△BDE的面积是28；

(2)∵DE∥AC，

∴ ,

∴AC= ED，

∵FE:ED=2:1，

∴EF=2ED，

∴ ；

(3)∵△BDE的面积是28，

∴S =14，

∴四边形ACDE的面积是35，

∴S =21，

∵DE∥AC，

∴△GEF∽△GAC，

∴ ，

∴S = ×21=9.