题目内容
已知直线y=x+6交x轴于点A,交y轴于点C,经过A和原点O的抛物线y=ax2+bx(a<0)的顶点B在直线AC上.

(1)求抛物线的函数关系式;
(2)以B点为圆心,以AB为半径作⊙B,将⊙B沿x轴翻折得到⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙B优弧 上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
上一动点,连结AE、OE,问在抛物线上是否存在一点M,使∠MOA︰∠AEO=2︰3,若存在,试求出点M的坐标;若不存在,试说明理由.
(1)该抛物线的函数关系式为y=﹣ x2﹣2x;
x2﹣2x;
(2)相切,理由见解析;
(3)存在这样的点M ,M的坐标为(﹣6+ ,﹣1+2
,﹣1+2 )或(﹣6﹣
)或(﹣6﹣ ,﹣1﹣2
,﹣1﹣2 ).
).
【解析】
试题分析:(1)根据过A、C两点的直线的解析式即可求出A,C的坐标,根据A,O的坐标即可得出抛物线的对称轴的解析式,然后将A点坐标代入抛物线中,联立上述两式即可求出抛物线的解析式.
(2)直线与圆的位置关系无非是相切与否,可连接AD,证AD是否与AC垂直即可.由于B,D关于x轴对称,那么可得出∠CAO=∠DAO=45°,因此可求出∠DAB=90°,即DA⊥AC,因此AC与圆D相切.
(3)根据圆周角定理可得出∠AEO=45°,那么∠MOA=30°,即M点的纵坐标的绝对值和横坐标的绝对值的比为tan30°,由此可得出x,y的比例关系式,然后联立抛物线的解析式即可求出M点的坐标.(要注意的是本题要分点M在x轴上方还是下方两种情况进行求解).
试题解析:(1)根据题意知:A(﹣6,0),C(0,6)
∵抛物线y=ax2+bx(a<0)经过A(﹣6,0),0(0,0).
∴对称轴x= =﹣3,b=6a…①
=﹣3,b=6a…①
当x=﹣3时,代入y=x+6得y=﹣3+6=3,
∴B点坐标为(﹣3,3).
∵点B在抛物线y=ax2+bx上,
∴3=9a﹣3b…②
结合①②解得a=﹣ ,b=﹣2,
,b=﹣2,
∴该抛物线的函数关系式为y=﹣ x2﹣2x;
x2﹣2x;
(2)相切
理由:连接AD,
∵AO=OC
∴∠ACO=∠CAO=45°
∵⊙B与⊙D关于x轴对称
∴∠BAO=∠DAO=45°
∴∠BAD=90°
又∵AD是⊙D的半径,
∴AC与⊙D相切.
∵抛物线的函数关系式为y=﹣ x2﹣2x,
x2﹣2x,
∴函数顶点坐标为(﹣3,3),
由于D、B关于x轴对称,
则BD=3×2=6;
(3)存在这样的点M.
设M点的坐标为(x,y)
∵∠AEO=∠ACO=45°
而∠MOA:∠AEO=2:3
∴∠MOA=30°
当点M在x轴上方时, =tan30°=
=tan30°= ,
,
∴y=﹣ x.
x.
∵点M在抛物线y=﹣ x2﹣2x上,
x2﹣2x上,
∴﹣ x=﹣
x=﹣ x2﹣2x,
x2﹣2x,
解得x=﹣6+ ,x=0(不合题意,舍去)
,x=0(不合题意,舍去)
∴M(﹣6+ ,﹣1+2
,﹣1+2 ).
).
当点M在x轴下方时, =tan30°=
=tan30°= ,
,
∴y= x,
x,
∵点M在抛物线y=﹣ x2﹣2x上.
x2﹣2x上.
∴ x=﹣
x=﹣ x2﹣2x,
x2﹣2x,
解得x=﹣6﹣ ,x=0(不合题意,舍去).
,x=0(不合题意,舍去).
∴M(﹣6﹣ ,﹣1﹣2
,﹣1﹣2 ),
),
∴M的坐标为(﹣6+ ,﹣1+2
,﹣1+2 )或(﹣6﹣
)或(﹣6﹣ ,﹣1﹣2
,﹣1﹣2 ).
).
 .
.
考点:二次函数综合题.

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案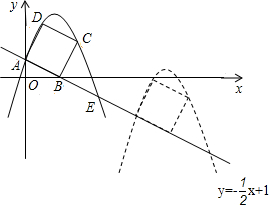
 (2013•梧州模拟)如图,已知直线y=
(2013•梧州模拟)如图,已知直线y= 轴交于点E(点E在抛物线对称轴的右侧).设点P运动时间为t秒.
轴交于点E(点E在抛物线对称轴的右侧).设点P运动时间为t秒. (2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9
(2010•资阳)如图,已知直线y=2x+2交y轴于点A,交x轴于点B,直线l:y=-3x+9 如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.
如图,已知直线l1与l2交于一点P,l1的函数表达式是y=2x+3,l2的函数表达式是y=kx+b(k≠0).点P的横坐标是-1,且l2与y轴的交点A的纵坐标也是-1.