题目内容

14．如图，⊙O中，OD⊥BC，∠CAD=40°，则∠BOD的度数是（　　）
A．40°B．50°C．60°D．80°

分析 由圆周角定理求出∠COD=2∠CAD=80°，由垂径定理得出$\widehat{BD}=\widehat{CD}$，再由圆心角、弧、弦的关系定理得出∠BOD=∠COD=80°即可．

解答 解：∵∠CAD=40°，
∴∠COD=2∠CAD=80°，
∵OD⊥BC，
∴$\widehat{BD}=\widehat{CD}$，
∴∠BOD=∠COD=80°，
故选：D．

点评 本题考查了圆周角定理、垂径定理、圆心角、弧、弦的关系定理；熟练掌握圆周角定理，由垂径定理得出弧相等是解决问题的关键．

练习册系列答案
相关题目
4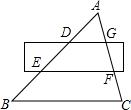．如图，△ABC被一平行于BC的矩形所截，AB被截成三等分，若△ADG的面积为a，则图中四边形DEFG的面积是（　　）
A．aB．2aC．3aD．4a
5．计算：（x-2y）7÷（2y-x）6=x-2y；${（-\frac{2}{3}）^{2009}}×{（1\frac{1}{2}）^{2009}}$=-1．
2．一堆足够多的棋子，其数目是3的倍数，现在依次进行如下操作：
第一步：将棋子平均分成左、中、右三堆；
第二步：从左堆中取出5枚棋子放入中堆，再从右堆中取出3枚棋子放入中堆；
第三步：从中堆取出与左堆余留棋子数相等的棋子放入左堆．
（1）若这堆棋子数为30，第三步完成后，中堆有多少枚棋子？
（2）若将题中第二步改为从左堆中取出8枚放入中堆，再从右堆中取出4枚放入中堆，其余步骤不变，则完成第三步后，中堆有多少枚棋子？（要有计算过程）
（3）若题中第三步完成后，中堆棋子共有9枚，则第二步应从左堆、右堆各取多少枚棋子放入中堆？
9．分解因式：
（1）x3-x；
（2）x（x-y）+y（y-x）．
19．如图，已知圆锥的母线长为9m，底面半径是4m，则圆锥的侧面积是36πm2．
6．解方程
（1）x2-2x-8=0
（2）（x-2）（x-5）=-2
（3）（3x-1）2=（x+1）2  
（4）x2-4x+1=0 （用配方法）
3．已知：①对顶角相等；②一条直线截两条平行直线所得的同位角相等；③两条直线被第三条直线所截，若同位角相等，则这两条直线平行．
（1）若要说明“两直线平行，内错角相等”成立，需要用到已知条件中的①②（填入序号即可）；
（2）根据（1）中的选择，请你说明“两直线平行，内错角相等”成立．
4．认真阅读下列解答过程：
比较2-$\sqrt{3}$与$\sqrt{3}$-$\sqrt{2}$的大小．
解：∵2-$\sqrt{3}$=（2-$\sqrt{3}$）•$\frac{2+\sqrt{3}}{2+\sqrt{3}}$=$\frac{1}{2+\sqrt{3}}$，
$\sqrt{3}$-$\sqrt{2}$=（$\sqrt{3}$-$\sqrt{2}$）•$\frac{\sqrt{3}+\sqrt{2}}{\sqrt{3}+\sqrt{2}}$=$\frac{1}{\sqrt{3}+\sqrt{2}}$，
又2+$\sqrt{3}$＞$\sqrt{3}$$+\sqrt{2}$＞0，∴$\frac{1}{2+\sqrt{3}}$＜$\frac{1}{\sqrt{3}+\sqrt{2}}$，
即2-$\sqrt{3}$＜$\sqrt{3}$-$\sqrt{2}$．
请仿照上述方法比较$\sqrt{6}$-$\sqrt{5}$与$\sqrt{5}$-2的大小关系．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网